题目内容
在平面直角坐标系xoy中,椭圆C的方程为
+y2=1.
(1)若一直线与椭圆C交于两不同点M,N,且线段MN恰以点(-1,-
)为中点,求直线MN的方程;
(2)过椭圆右焦点F做直线l与椭圆交于不同的两点A,B,设
=λ
,点T坐标为(2,0),若λ∈[-3,-2],求|
+
|的取值范围.
| x2 |
| 2 |
(1)若一直线与椭圆C交于两不同点M,N,且线段MN恰以点(-1,-
| 1 |
| 4 |
(2)过椭圆右焦点F做直线l与椭圆交于不同的两点A,B,设
| FA |
| FB |
| TA |
| TB |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先判断直线MN与椭圆必有公共点,再利用点差法得到中点坐标与直线斜率的关系式,即可求直线MN的方程;
(2)设直线l的方程代入椭圆方程,得到一元二次方程,进而利用向量的关系得到|
+
|2=(x3+x4-4)2+(y3+y4)2=16-
+
,换元即可求|
+
|的取值范围.
(2)设直线l的方程代入椭圆方程,得到一元二次方程,进而利用向量的关系得到|
| TA |
| TB |
| 28 |
| m2+2 |
| 8 |
| (m2+2)2 |
| TA |
| TB |
解答:
解:(1))∵点(-1,-
)在椭圆内部,∴直线MN与椭圆必有公共点,
令点M(x1,y1),N(x2,y2),
代入椭圆方程中,
+y12=1,
+y22=1,
两式作差,因式分解有:
=-(y1-y2)(y1+y2)
由中点坐标可得:x1+x2=-2,y1+y2=-
,
解得
=-2,
∴直线MN的方程为y=-2x-
;
(2)由题意容易验证直线l的斜率不为0,故可设直线l的方程为x=my+1,且设点A(x3,y3),B(x4,y4),
代入
+y2=1中,得(m2+2)y2+2my-1=0.
∴y3+y4=-
①,y3y4=-
②,
∵
=λ
,∴
=λ且λ<0,
∴将上式①的平方除以②,得λ+
+2=-
,
由λ∈[-3,-2],可得-
≤λ+
+2≤
,
∴-
≤-
≤
,
∴
≤m2≤1,
∵
=(x3-2,y3),
=(x4-2,y4),
∴|
+
|2=(x3+x4-4)2+(y3+y4)2=16-
+
.
令t=
,则
≤t≤
,
∴|
+
|2=16-28t+8t2=8(t-
)2-
,
∵
≤t≤
,
∴|
+
|2∈[
,
],
∴|
+
|∈[
,
].
| 1 |
| 4 |
令点M(x1,y1),N(x2,y2),
代入椭圆方程中,
| x12 |
| 2 |
| x22 |
| 2 |
两式作差,因式分解有:
| (x1-x2)(x1+x2) |
| 2 |
由中点坐标可得:x1+x2=-2,y1+y2=-
| 1 |
| 2 |
解得
| y1-y2 |
| x1-x2 |
∴直线MN的方程为y=-2x-
| 9 |
| 4 |
(2)由题意容易验证直线l的斜率不为0,故可设直线l的方程为x=my+1,且设点A(x3,y3),B(x4,y4),
代入
| x2 |
| 2 |
∴y3+y4=-
| 2m |
| m2+2 |
| 1 |
| m2+2 |
∵
| FA |
| FB |
| y3 |
| y4 |
∴将上式①的平方除以②,得λ+
| 1 |
| λ |
| 4m2 |
| m2+2 |
由λ∈[-3,-2],可得-
| 4 |
| 3 |
| 1 |
| λ |
| 1 |
| 2 |
∴-
| 4 |
| 3 |
| 4m2 |
| m2+2 |
| 1 |
| 2 |
∴
| 2 |
| 7 |
∵
| TA |
| TB |
∴|
| TA |
| TB |
| 28 |
| m2+2 |
| 8 |
| (m2+2)2 |
令t=
| 1 |
| m2+2 |
| 1 |
| 3 |
| 7 |
| 16 |
∴|
| TA |
| TB |
| 7 |
| 4 |
| 17 |
| 2 |
∵
| 1 |
| 3 |
| 7 |
| 16 |
∴|
| TA |
| TB |
| 169 |
| 32 |
| 68 |
| 9 |
∴|
| TA |
| TB |
13
| ||
| 8 |
2
| ||
| 3 |
点评:本题主要考查了直线与椭圆的位置关系综合运用,考查点差法,考查向量知识的运用,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
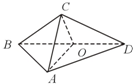 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:①AC⊥BD;
②AD⊥CO;
③△AOC为正三角形;
④cos∠ADC=
| ||
| 4 |
⑤四面体ABCD的外接球面积为32π.
其中真命题是( )
| A、②③④ | B、①③④ |
| C、①④⑤ | D、①③⑤ |
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )
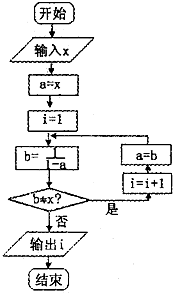

| A、3 | B、5 | C、6 | D、8 |