题目内容
已知函数f（x）=
的定义域为（0，+∞），值域为[2，+∞），则实数k的取值范围是 ．
| x2-2kx+k2+1 |
| x-k |
考点：函数的值域,函数的定义域及其求法
专题：函数的性质及应用
分析：式子进行变形为后，利用双勾函数的性质得出x与k的关系，再根据x的取值范围即能求出k的取值范围．
解答：
解：f（x）=
=
=(x-k)+
，
∵函数的值域为[2，+∞），
∴
，得（x-k）2=1，
x-k=1，∴k=x-1，又∵x∈（0，+∞），∴k＞-1，即k的取值范围是（-1，+∞）．
故答案为：（-1，+∞）．
| x2-2kx+k2+1 |
| x-k |
| (x-k)2+1 |
| x-k |
| 1 |
| x-k |
∵函数的值域为[2，+∞），
∴
|
x-k=1，∴k=x-1，又∵x∈（0，+∞），∴k＞-1，即k的取值范围是（-1，+∞）．
故答案为：（-1，+∞）．
点评：由值域得出x-k满足的条件，再根据双勾函数的性质，就能求出k的取值范围．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
正三棱柱的左视图如图所示，则该正三棱柱的侧面积为（ ）
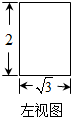
| A、4 | ||||
| B、12 | ||||
C、
| ||||
| D、24 |
一个算法的程序框图如图所示，如果输入的x的值为2014，则输出的i的结果为（ ）
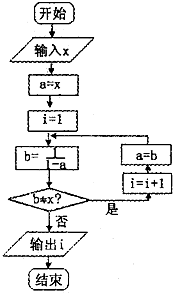
| A、3 | B、5 | C、6 | D、8 |