Question

设f（x）=|2-x²|，若b＞a＞0，且f（a）=f（b），则a²+b的取值范围为

 

．

Answer 1

考点：函数的零点

专题：计算题,作图题,函数的性质及应用

分析：由题意作出函数的图象，可得f（a）=2-a²，f（b）=b²-2，（0＜a＜

2

），从而得到a²+b=a²+

4-a2

，利用换元法求其取值范围．

解答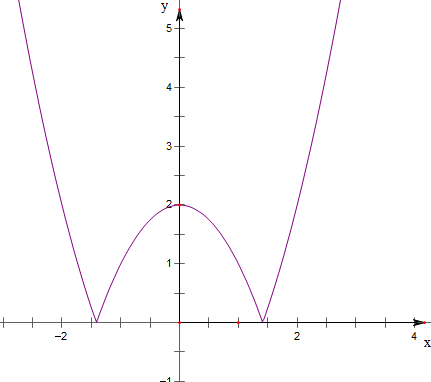： 解：f（x）=|2-x²|的图象如右图，
则由题意可知，
f（a）=2-a²，f（b）=b²-2，（0＜a＜

2

），
由f（a）=f（b）可得，
b=

4-a2

，
故a²+b=a²+

4-a2

，
令

4-a2

=t，则

2

＜t＜2，
a²=4-t²，
故a²+b=4-t²+t
=-（t-

1

2

）²+4+

1

4

，
故a²+b=4-t²+t在（

2

，2）上单调递减，
故2＜a²+b＜2+

2

，
故答案为：（2，2+

2

）．

点评：本题考查了函数图象的作法及换元法求取值范围，属于中档题．