题目内容
已知抛物线x2=2py(p>0),抛物线上一点A(a,4)到抛物线旳准线的距离为5.
(1)求抛物线的方程;
(2)过点M(2,-1)作抛物线的两条切线,切点分别为B,C,求证:MB⊥MC.
(1)求抛物线的方程;
(2)过点M(2,-1)作抛物线的两条切线,切点分别为B,C,求证:MB⊥MC.
考点:抛物线的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意
+4=5,由此能求出抛物线的标准方程.
(2)由x2=4y,得y′=
x,从而x2=4y在点(x0,
)处的切线方程为y-
=
(x-x0),把点M(2,-1)代入,得x02-4x0-4=0,从而B(2+2
,4+2
),C(2-2
,4-2
),由此能证明MB⊥MC.
| p |
| 2 |
(2)由x2=4y,得y′=
| 1 |
| 2 |
| x02 |
| 4 |
| x02 |
| 4 |
| x0 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:
(1)解:由题意抛物线的方程为x2=2py(p>0),
因为点A(a,4)在抛物线上,
又点A(a,4)到抛物线准线的距离是5,
所以
+4=5,解得p=2.
所以抛物线的标准方程为x2=4y.
(2)证明:∵x2=4y,∴y′=
x,
∴x2=4y在点(x0,
)处的切线方程为y-
=
(x-x0),
把点M(2,-1)代入,得x02-4x0-4=0,
解得
,或
,
∴B(2+2
,4+2
),C(2-2
,4-2
),
∴kMB=
,kMC=
,
∴kMB•kMC=
×
=-1,
∴MB⊥MC.
因为点A(a,4)在抛物线上,
又点A(a,4)到抛物线准线的距离是5,
所以
| p |
| 2 |
所以抛物线的标准方程为x2=4y.
(2)证明:∵x2=4y,∴y′=
| 1 |
| 2 |
∴x2=4y在点(x0,
| x02 |
| 4 |
| x02 |
| 4 |
| x0 |
| 2 |
把点M(2,-1)代入,得x02-4x0-4=0,
解得
|
|
∴B(2+2
| 2 |
| 2 |
| 2 |
| 2 |
∴kMB=
4+2
| ||
2
|
4-2
| ||
-2
|
∴kMB•kMC=
4+2
| ||
2
|
4-2
| ||
-2
|
∴MB⊥MC.
点评:本题考查抛物线标准方程的求法,考查两直线垂直的证明,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
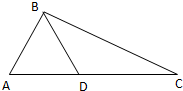
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
BD,BC=2BD,则sinC的值为( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在平行四边形ABCD中,
-
-
+
等于( )
| AB |
| AC |
| CA |
| CD |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
集合 A={1,2,3,4,5},B={1,2,3},C={z|z=xy,x∈A且y∈B},则集合C中的元素个数为( )
| A、3 | B、11 | C、8 | D、12 |