Question

已知正五边形边长是1，求它的外接圆半径．

Answer 1

考点：弧长公式

专题：三角函数的求值

分析：如图所示，正五边形的半径OA=

1 2

sin36°

=

1

2sin36°

．由于sin36°=cos54°，可得2sin18°cos18°=4cos³18°-3cos18°，化为4sin²18°+2sin18°-1=0，
解得sin18°=

5 -1

4

．即可得出．

解答： 解：如图所示，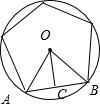
正五边形的半径OA=

1 2

sin36°

=

1

2sin36°

．
∵sin36°=cos54°，
∴2sin18°cos18°=4cos³18°-3cos18°，
化为2sin18°=4cos²18°-3，
∴4sin²18°+2sin18°-1=0，
解得sin18°=

5 -1

4

．
∴OA=

1

4sin18°cos18°

=

1

( 5 -1) 1-( 5 -1 4 )2

=

5 +1

10+2 5

．

点评：本题考查了直角三角形的边角关系、倍角公式、同角三角函数基本关系式，考查了计算能力，属于中档题．