题目内容
在平行四边形ABCD中，
-
-
+
等于（ ）
| AB |
| AC |
| CA |
| CD |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
考点：向量的三角形法则
专题：平面向量及应用
分析：在平行四边形ABCD中，可得
=
，即可得出．
| AB |
| DC |
解答：
解：在平行四边形ABCD中，可得
=
，
∴
-
-
+
=
-
=
．
故选：D．
| AB |
| DC |
∴
| AB |
| AC |
| CA |
| CD |
| CA |
| CA |
| 0 |
故选：D．
点评：本题考查了平行四边形的性质、向量相等、向量的三角形法则，属于基础题．
练习册系列答案
相关题目
已知全集U=R，集合A={x|x≥
}，集合B={x|x≤1}，那么∁U（A∩B）=（ ）
| 1 |
| 2 |
A、{x|x≤
| ||
B、{x|x＜
| ||
C、{x|x＜
| ||
D、{x|x≤＜
|
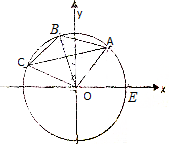如图，已知单位圆上有四点E（1，0），A（cosθ，sinθ），B（cos2θ，sin2θ），C（cos3θ，sin3θ）（0＜θ≤