题目内容
已知logkx，logmx，lognx满足关系式2logmx=logkx+lognx，（x≠1），证明：n2=（kn） logkm．
考点：对数的运算性质
专题：函数的性质及应用
分析：logkx，logmx，lognx满足关系式2logmx=logkx+lognx，（x≠1），可得
=
+
，化为lgn2=logkmlg（kn），即可得出．
| 2lgx |
| lgm |
| lgx |
| lgk |
| lgx |
| lgn |
解答：
证明：∵logkx，logmx，lognx满足关系式2logmx=logkx+lognx，（x≠1），
∴
=
+
，
化为2lgklgn=lgm（lgk+lgn）=lgm•lg（kn），
∴lgn2=logkmlg（kn），
∴n2=(kn)logkm．
∴
| 2lgx |
| lgm |
| lgx |
| lgk |
| lgx |
| lgn |
化为2lgklgn=lgm（lgk+lgn）=lgm•lg（kn），
∴lgn2=logkmlg（kn），
∴n2=(kn)logkm．
点评：本题考查了对数的运算法则、对数的换底公式、指数式与对数式的互化，属于基础题．
练习册系列答案
相关题目
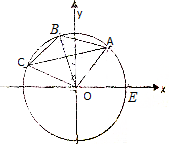如图，已知单位圆上有四点E（1，0），A（cosθ，sinθ），B（cos2θ，sin2θ），C（cos3θ，sin3θ）（0＜θ≤过点P（3，2）与双曲线
-
=1有且只有一个公共点的直线有（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、一条 | B、二条 | C、三条 | D、四条 |