题目内容
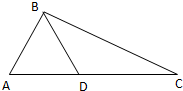
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
BD,BC=2BD,则sinC的值为( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理
专题:解三角形
分析:设BD=a,则由题意可得:BC=2a,AB=AD=
a,利用余弦定理表示出cosA,把三边长代入求出cosA的值,进而确定出sinA的值,由AB,BC,以及sinA的值,利用正弦定理求出sinC的值即可.
| ||
| 2 |
解答:
解:设BD=a,则由题意可得:BC=2a,AB=AD=
a,
在△ABD中,由余弦定理得:cosA=
=
=
,
∴sinA=
=
,
在△ABC中,由正弦定理得,
=
,即
=
,
解得:sinC=
,
故选:D.
| ||
| 2 |
在△ABD中,由余弦定理得:cosA=
| AB2+AD2-BD2 |
| 2AB•AD |
2×
| ||||
2×(
|
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
2
| ||
| 3 |
在△ABC中,由正弦定理得,
| AB |
| sinC |
| BC |
| sinA |
| ||||
| sinC |
| 2a | ||||
|
解得:sinC=
| ||
| 6 |
故选:D.
点评:此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知函数f(x)=2x,则函数y=f-1(1-x)的大致图象是( )
A、 |
B、 |
C、 |
D、 |
已知全集U=R,集合A={x|x≥
},集合B={x|x≤1},那么∁U(A∩B)=( )
| 1 |
| 2 |
A、{x|x≤
| ||
B、{x|x<
| ||
C、{x|x<
| ||
D、{x|x≤<
|
| 2 |
| 2 |
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、±1 |
已知
=
,则
=( )
| cosα |
| sinα-1 |
| 1 |
| 2 |
| 1+sinα |
| cosα |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |