题目内容
有三个新兴城镇，分别位于A、B、C三个点处，且AB=AC=13千米，BC=10千米．今计划合建一个中心医院．为同时方便三个城镇，需要将医院建在BC的垂直平分线上的点P处．若希望点P到三个城镇距离的平方和最小，点P应该位于何处？
考点：二次函数的性质
专题：函数的性质及应用
分析：首先根据题意巧妙建立平面直角坐标系，然后建立关系式，利用二次函数的问题求解．
解答：
解：根据题意：以BC中点为原点，BC所在直线为x轴，建立坐标系，
则B（-5，0），C（5，0），A（012），设P（0，y）
∴PA2+PB2+PC2=2（25+y2）+（12-y）2=3（y-4）2+146
∴y=4时取最小值146，
此时P的坐标为：（0，4）
故答案为：（0，4）
则B（-5，0），C（5，0），A（012），设P（0，y）
∴PA2+PB2+PC2=2（25+y2）+（12-y）2=3（y-4）2+146
∴y=4时取最小值146，
此时P的坐标为：（0，4）
故答案为：（0，4）
点评：本题考查的知识点：建立平面直角坐标系的技巧，两点间的距离公式，二次函数的顶点式与一般式的互化．
练习册系列答案
相关题目
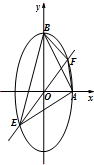已知椭圆C：