题目内容
已知函数f(x)=-
x3-
ax2+2x,讨论f(x)的单调性..
| 1 |
| 3 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的导数,利用函数的单调性和导数之间的关系即可判断函数的单调性.
解答:
解:f′(x)=x2-ax+2,
①当△=a2-8≤0即-2
≤a≤2
时f(x)=-
x3-
ax2+2x 在R内单调递增,
②当△=a2-8>0即a<-2
或a>2
时
解f′(x)=0得x1=
,x2=
,
∴函数的增区间为(-∞,
)和(
,+∞),
减区间为[
,
].
①当△=a2-8≤0即-2
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
②当△=a2-8>0即a<-2
| 2 |
| 2 |
解f′(x)=0得x1=
a-
| ||
| 2 |
a+
| ||
| 2 |
∴函数的增区间为(-∞,
a-
| ||
| 2 |
a+
| ||
| 2 |
减区间为[
a-
| ||
| 2 |
a+
| ||
| 2 |
点评:本题主要考查函数单调性和导数之间的关系,注意讨论a的取值范围对函数导数的影响.

练习册系列答案
相关题目
如图中阴影部分表示的集合是( )


| A、B∩CUA |
| B、A∩(CUB) |
| C、CU(A∩B) |
| D、CU(A∪B) |
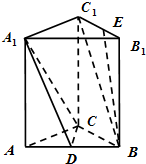 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点, 成都七中学生会经过综合考评,新招了14名男生和6名女生到学生会工作,茎叶图表示这20名同学的测试成绩(单位:分),规定:成绩在180分以上者到“M部门”工作;成绩在180分以下者到“N部门”工作.
成都七中学生会经过综合考评,新招了14名男生和6名女生到学生会工作,茎叶图表示这20名同学的测试成绩(单位:分),规定:成绩在180分以上者到“M部门”工作;成绩在180分以下者到“N部门”工作.