题目内容
已知函数y=-x2+2x，若a≤x≤b时，a≤y≤b，试求实数a，b的值．
考点：二次函数的性质
专题：函数的性质及应用
分析：利用二次函数的对称轴与区间的位置关系决定区间的单调性，讨论解答．
解答：
解：①当b≤1时，函数y=-x2+2x在a≤x≤b是增函数，此时x=a时，ymin=a，x=b时，ymax=b，即-a2+2a=a，-b2+2b=b解得a=0，b=1；
②当a≥1时，y=-x2+2x，在a≤x≤b是减函数，∵a≤y≤b，∴-a2+2a=b，-b2+2b=a，整理得b2-3b+3=0无解；
③当a＜1＜b时，最大值为b=1与b＞1矛盾；
综上，a=0，b=1．
②当a≥1时，y=-x2+2x，在a≤x≤b是减函数，∵a≤y≤b，∴-a2+2a=b，-b2+2b=a，整理得b2-3b+3=0无解；
③当a＜1＜b时，最大值为b=1与b＞1矛盾；
综上，a=0，b=1．
点评：本题考查了二次函数的单调性与对称轴的关系，如果对称轴一定，区间不定，则需要分类讨论．
练习册系列答案
相关题目
二项式（
+
）10展开式中的常数项是（ ）
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
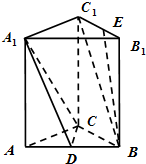如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1，点D是AB的中点，