题目内容
已知二项式（1+3x）n的各项系数和为256，则(
+
)n的常数项为 ．
| x |
| 1 | ||
|
考点：二项式系数的性质
专题：二项式定理
分析：根据题意，求出n的值，再利用二项展开式的通项Tr+1求出展开式中常数项即可．
解答：
解：∵二项式（1+3x）n的各项系数和为256，
即（1+3）n=256，
∴n=4；
∴(
+
)n的展开式的通项是
Tr+1=
•(
)4-r•(
)r=
•(
)4-2r，
令4-2r=0，解得r=2；
∴展开式中常数项是T2+1=
=6．
故答案为：6．
即（1+3）n=256，
∴n=4；
∴(
| x |
| 1 | ||
|
Tr+1=
| C | r 4 |
| x |
| 1 | ||
|
| C | r 4 |
| x |
令4-2r=0，解得r=2；
∴展开式中常数项是T2+1=
| C | 2 4 |
故答案为：6．
点评：本题考查了二项式定理的应用问题，解题时要区分二项式系数与二项展开式各项的系数是什么，属于基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
二项式（
+
）10展开式中的常数项是（ ）
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
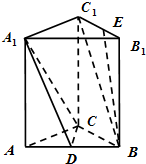如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1，点D是AB的中点，