题目内容
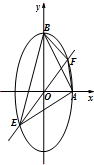 已知椭圆C:
已知椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| 2 |
(1)求椭圆C的方程;
(2)当四边形AEBF面积取最大值时,求k的值.
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)通过椭圆的离心率,直线与圆相切,求出a,b即可求出椭圆的方程.
(2)设E(x1,kx1),F(x2,kx2),其中x1<x2,将y=kx代入椭圆的方程x2+
=1,利用韦达定理,结合点E,F到直线AB的距离分别,表示出四边形AEBF的面积,利用基本不等式求出四边形AEBF面积的最大值时的k值即可.
(2)设E(x1,kx1),F(x2,kx2),其中x1<x2,将y=kx代入椭圆的方程x2+
| y2 |
| 4 |
解答:
解:(1)由题意知:e=
=
∴e2=
=
=
,∴a2=4b2.…(2分)
又∵圆x2+y2=b2与直线x-y+
=0相切,∴b=1,∴a2=4,…(3分)
故所求椭圆C的方程为x2+
=1…(4分)
(2)设E(x1,kx1),F(x2,kx2),其中x1<x2,
将y=kx代入椭圆的方程x2+
=1整理得:(k2+4)x2=4,
故x2=-x1=
.①…(5分)
又点E,F到直线AB的距离分别为h1=
=
,h2=
=
.|AB|=
=
…(7分)
所以四边形AEBF的面积为S=
|AB|(h1+h2)=
•
•
=
…(9分)
=2
=2
=2
≤2
,…(11分)
当k2=4(k>0),即当k=2时,上式取等号.
所以当四边形AEBF面积的最大值时,k=2.…(12分)
| c |
| a |
| ||
| 2 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
又∵圆x2+y2=b2与直线x-y+
| 2 |
故所求椭圆C的方程为x2+
| y2 |
| 4 |
(2)设E(x1,kx1),F(x2,kx2),其中x1<x2,
将y=kx代入椭圆的方程x2+
| y2 |
| 4 |
故x2=-x1=
| 2 | ||
|
又点E,F到直线AB的距离分别为h1=
| |2x1+kx1-2| | ||
|
2(2+k+
| ||
|
| |2x2+kx2-2| | ||
|
2(2+k-
| ||
|
| 22+1 |
| 5 |
所以四边形AEBF的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4(2+k) | ||
|
| 2(2+k) | ||
|
=2
|
1+
|
1+
|
| 2 |
当k2=4(k>0),即当k=2时,上式取等号.
所以当四边形AEBF面积的最大值时,k=2.…(12分)
点评:本题考查直线与椭圆的位置关系,圆锥曲线的综合应用,考查分析问题解决问题的能力,转化思想以及计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
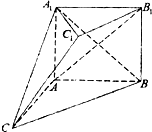 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=