题目内容
设定义在R上的函数f(x)对于任意x、y都有f(x+y)=f(x)+f(y)成立,且f(1)=-2,当x>0时,f(x)<0.(1)判断并证明函数f(x)的奇偶性;
(2)判断并证明f(x)在R上的单调性;
(3)当x∈[-2014,2014],求函数f(x)的最大值.
(2)判断并证明f(x)在R上的单调性;
(3)当x∈[-2014,2014],求函数f(x)的最大值.
考点:函数的最值及其几何意义,函数单调性的判断与证明,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(1)令x=y=0求出f(0)=0,再令y=-x代入式子化简,结合函数奇偶性的定义,可得f(x)是奇函数;
(2)设x1<x2,结合f(x+y)=f(x)+f(y)可得f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),由x>0时,有f(x)>0,可得f(x2)>f(x1),证明函数在R上单调递减;
(3)再利用赋值法和条件,分别求出函数最大值和最小值.
(2)设x1<x2,结合f(x+y)=f(x)+f(y)可得f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),由x>0时,有f(x)>0,可得f(x2)>f(x1),证明函数在R上单调递减;
(3)再利用赋值法和条件,分别求出函数最大值和最小值.
解答:
解:(1)令x=y=0,可得f(0)=0,
令y=-x,则f(0)=f(-x)+f(x),
∴f(-x)=-f(x),∴f(x)为奇函数,
(2)设x1<x2,令y=-x1,x=x2
则f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),
因为x>0时,f(x)<0,
故f(x2-x1)<0,即f(x2)-f(x1)<0.
∴f(x2)<f(x1),
∴f(x)在R上单调递减;
(3)f(x)在[-2014,2014]上单调递减,
∴x=-2014时,f(x)有最大值-2014f(1)=4028,
x=2014时,f(x)有最小值为f(2014)=-4028.
令y=-x,则f(0)=f(-x)+f(x),
∴f(-x)=-f(x),∴f(x)为奇函数,
(2)设x1<x2,令y=-x1,x=x2
则f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(x1),
因为x>0时,f(x)<0,
故f(x2-x1)<0,即f(x2)-f(x1)<0.
∴f(x2)<f(x1),
∴f(x)在R上单调递减;
(3)f(x)在[-2014,2014]上单调递减,
∴x=-2014时,f(x)有最大值-2014f(1)=4028,
x=2014时,f(x)有最小值为f(2014)=-4028.
点评:本题考查抽象函数的性质,涉及函数奇偶性、单调性的判断,以及函数最值,解此类题目,注意赋值法的运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
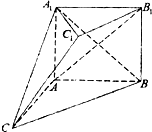 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=