题目内容
当x<1,a>-1,关于x的式子
的最大值为-4,求a的值及取得最大值时x的值.
| x2-2x+a+2 |
| x-1 |
考点:函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:化简
=
=(x-1)+
=-[[-(x-1)]+(-
)],对[-(x-1)]+(-
)利用基本不等式求值.
| x2-2x+a+2 |
| x-1 |
| (x-1)2+a+1 |
| x-1 |
| a+1 |
| x-1 |
| a+1 |
| x-1 |
| a+1 |
| x-1 |
解答:
解:
=
=(x-1)+
,
∵x<1,a>-1,
∴x-1<0,
<0,
则[-(x-1)]+(-
)≥2
,
(当且仅当(x-1)2=a+1时,等号成立),
又∵
的最大值为-4,
∴2
=4,
则a=3,从而得最大值时,x=-1.
| x2-2x+a+2 |
| x-1 |
| (x-1)2+a+1 |
| x-1 |
=(x-1)+
| a+1 |
| x-1 |
∵x<1,a>-1,
∴x-1<0,
| a+1 |
| x-1 |
则[-(x-1)]+(-
| a+1 |
| x-1 |
| a+1 |
(当且仅当(x-1)2=a+1时,等号成立),
又∵
| x2-2x+a+2 |
| x-1 |
∴2
| a+1 |
则a=3,从而得最大值时,x=-1.
点评:本题考查了学生的化简能力与转化为基本不等式的形式,从而借助基本不等式求解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
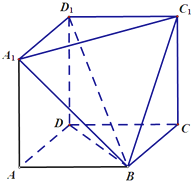 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.