题目内容
已知正数x，y满足
+
=1，若xy≥m恒成立，求m的取值范围．
| 4 |
| x |
| 9 |
| y |
考点：函数恒成立问题
专题：不等式的解法及应用
分析：直接利用基本不等式结合已知条件求得xy的最小值，则答案可求．
解答：
解：∵正实数x，y满足
+
=1，
∴1=
+
≥2
=12
，
∴
≥12，即xy≥144．
∴xy的最小值为144．
当且仅当正实数x，y满足
，即x=8，y=18时，xy取最小值144．
∴使xy≥m恒成立的m的取值范围是（-∞，144]．
| 4 |
| x |
| 9 |
| y |
∴1=
| 4 |
| x |
| 9 |
| y |
|
|
∴
| xy |
∴xy的最小值为144．
当且仅当正实数x，y满足
|
∴使xy≥m恒成立的m的取值范围是（-∞，144]．
点评：本题考查了函数恒成立问题，考查了利用基本不等式求最值，是中档题．
练习册系列答案
相关题目
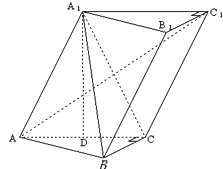在三棱柱ABC-A1B1C1中，∠BCA=90°，AC=BC=AA1=2，A1在底面ABC上的射影恰为AC的中点D．
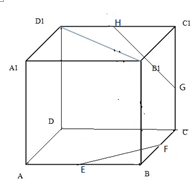如图，E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点．证明：FE、HG、DC三线共点．