Question

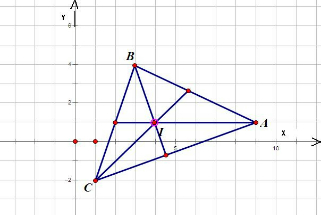
已知在△ABC中，定点A（9，1）、B（3，4），内心I（4，1），求顶点C的坐标．

Answer 1

考点：解三角形

专题：解三角形

分析：先求出AB方程即可再求出内切圆的半径r，设BC方程为y-4=k（x-3），利用内心到各边的距离均为内切圆的半径，可求直线BC的方程，同理得到直线AC的方程，联立即可解得C的坐标．

解答： 解：先求出AB斜率：k=

4-1

3-9

=-

1

2

故AB方程：y-4=（-

1

2

）（x-3）即：x+2y-11=0
再求出内切圆的半径r=

5

5

=

5

设BC方程为y-4=k（x-3）即：kx-y-3k+4=0
利用内心到各边的距离均为内切圆的半径，故

|4k-1-3k+4|

1+k2

=

5

解之：k=2或-

1

2

显然k=-

1

2

是AB的斜率
故BC：y-4=2（x-3）即2x-y-2=0
同理得到：AC：x-2y-7=0
联立AC，BC方程可以得到：C（1，-2）

点评：本题主要考察了三角形内心的特征，考察了直线的方程、斜率、相交等知识的应用，属于中档题．