题目内容
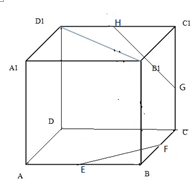如图，E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点．证明：FE、HG、DC三线共点．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：首先，设EF与DC共点于S'，DC与HG共点于S''，然后，通过证明三角形全等的方法证明S'与S''是同一个点，即可说明线共点．
解答：
解：如图所示，设EF与DC共点于S'，DC与HG共点于S''，
RT△CFS'≌RT△BFE，得到CS'=BE=
AB，
RT△CGS''≌RT△C1GH，得到CS''=C1H=
C1D1，
则，CS'=CS''（即S'与S''是同一个点），
∴EF、GH、DC三线共点．
RT△CFS'≌RT△BFE，得到CS'=BE=
| 1 |
| 2 |
RT△CGS''≌RT△C1GH，得到CS''=C1H=
| 1 |
| 2 |
则，CS'=CS''（即S'与S''是同一个点），
∴EF、GH、DC三线共点．
点评：本题重点考查了空间中点线面的位置关系等知识，属于中档题，理解线共点问题的处理思路和方法是解题关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
设函数f（x）=x-
，对任意x∈[1，+∞），f（mx）+mf（x）＞0恒成立，则实数m的取值范围是（ ）
| 1 |
| x |
| A、（-∞，-1）∪（1，+∞） |
| B、（1，+∞） |
| C、（-∞，-1） |
| D、不能确定 |
过正棱台两底面中心的截面一定是（ ）
| A、直角梯形 | B、等腰梯形 |
| C、一般梯形或等腰梯形 | D、矩形 |
在各项均为正数的等比数列{an}中，
≤2，则下列结论中正确的是（ ）
| a3+a11 |
| a7 |
| A、数列{an}是常数列 |
| B、数列{an}是递增数列 |
| C、数列{an}是递减数列 |
| D、数列{an}有可能是递增数列也有可能是递减数列 |