Question

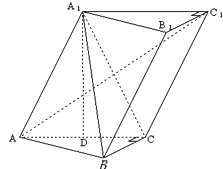在三棱柱ABC-A₁B₁C₁中，∠BCA=90°，AC=BC=AA₁=2，A₁在底面ABC上的射影恰为AC的中点D．
（1）求证：AC₁⊥BC；
（2）求二面角A₁-BC-A的大小；
（3）求CC₁到平面A₁AB的距离．

Answer 1

考点：点、线、面间的距离计算,二面角的平面角及求法

专题：空间位置关系与距离,空间角

分析：（1）A₁在底面ABC上的射影恰为AC的中点D，可得A₁D⊥平面ABC，A₁D⊥BC．又BC⊥AC，可得BC⊥平面ACC₁A₁，即可得出AC₁⊥BC．
（2）A₁在底面ABC上的射影恰为AC的中点D，BC⊥AC，利用三垂线定理可得BC⊥A₁C．可得∠A₁CD是二面角A₁-BC-A的平面角．在Rt△AA₁D中，利用勾股定理可得A₁D，CD=1．利用tan∠A₁CD=

A1D

CD

即可得出．
（3）连接BD．由于D是AC的中点，则CC₁到平面A₁AB的距离是点D到平面A₁AB的距离的2倍．利用VA1-ABD=VD-AA1B，可得

1

3

×A1D×S△ABD=

1

3

×hD×S△AA1B，即可得出h_D．

解答： （1）证明：∵A₁在底面ABC上的射影恰为AC的中点D，
∴A₁D⊥平面AB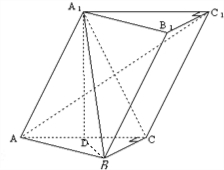C，
∴A₁D⊥BC．
∵BC⊥AC，A₁D∩AC=D．
∴BC⊥平面ACC₁A₁，
∵AC₁?平面ACC₁A₁，
∴AC₁⊥BC．
（2）解：∵A₁在底面ABC上的射影恰为AC的中点D，BC⊥AC，
∴BC⊥A₁C．
∴∠A₁CD是二面角A₁-BC-A的平面角．
在Rt△AA₁D中，A1D=

A A 2 1 -AD2

=

3

．
CD=1．
∴tan∠A₁CD=

A1D

CD

=

3

，
∴∠A₁CD=60°，即二面角A₁-BC-A是60°．
（3）解：连接BD．由于D是AC的中点，则CC₁到平面A₁AB的距离是点D到平面A₁AB的距离的2倍．
在Rt△BCD中，BD=

12+22

=

5

．
在Rt△A₁BD中，A₁B=

( 3 )2+( 5 )2

=2

2

．
在Rt△ACB中，AB=2

2

．
在△ABC中，S_△ABC=

1

2

×2×

(2 2 )2-12

=

7

．
又S△ABD=

1

2

S△ABC=

1

2

×

1

2

×22=1．
∵VA1-ABD=VD-AA1B，
∴

1

3

×A1D×S△ABD=

1

3

×hD×S△AA1B，
∴h_D=

3 ×1

7

=

21

7

．
∴CC₁到平面A₁AB的距离是

2 21

7

．

点评：本题考查了线面垂直的判定与性质定理、三垂线定理、勾股定理、三棱锥的体积计算公式、二面角的求法，考查了推理能力与计算能力，属于难题．