题目内容
函数f(x)=sin(-x+
),x∈(0,π)的单调增区间为 .
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性
专题:三角函数的图像与性质
分析:求三角函数的单调区间,一般要将自变量的系数变为正数,再由三角函数的单调性得出自变量所满足的不等式,求解即可得出所要的单调递增区间.
解答:
解:y=sin(
-x)=-sin(x-
)
令2kπ+
≤x-
≤2kπ+
,k∈Z解得2kπ+
≤x≤2kπ+
,k∈Z
函数的递增区间是[2kπ+
,2kπ+
](k∈Z),
当k=0时,函数的单调增区间为:[
,
],
∵x∈(0,π)∴函数的单调增区间为:[
,π).
故答案为:[
,π).
| π |
| 3 |
| π |
| 3 |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 6 |
| 11π |
| 6 |
函数的递增区间是[2kπ+
| 5π |
| 6 |
| 11π |
| 6 |
当k=0时,函数的单调增区间为:[
| 5π |
| 6 |
| 11π |
| 6 |
∵x∈(0,π)∴函数的单调增区间为:[
| 5π |
| 6 |
故答案为:[
| 5π |
| 6 |
点评:本题考查正弦函数的单调性,求解本题的关键有二,一是将自变量的系数为为正,二是根据正弦函数的单调性得出相位满足的取值范围,解题时不要忘记引入的参数的取值范围即k∈Z.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合A={0,1},B={-1,a2},则“a=1”是“A∩B={1}”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
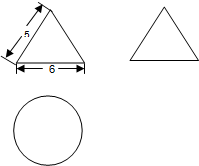 一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为(cm2\cm3)( )
一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为(cm2\cm3)( )| A、24π,12π |
| B、15π,12π |
| C、24π,36π |
| D、以上都不正确 |

