题目内容
已知函数f（x）=Asin（ωx+φ）（0＜ω＜3，0＜φ＜
，A＞0）的图象经过点P（0，2
），当x=-
时，f（x）取得最小值-4．
（1）求函数f（x）的解析式；
（2）f（x）的图象经过怎样的平移和伸缩变换，可以得到y=4sinx的图象？
| π |
| 2 |
| 3 |
| 5π |
| 12 |
（1）求函数f（x）的解析式；
（2）f（x）的图象经过怎样的平移和伸缩变换，可以得到y=4sinx的图象？
考点：函数y=Asin（ωx+φ）的图象变换,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（1）由函数的最值求出A，把特殊点的坐标代入函数解析式求出φ的值，再根据当x=-
时，f（x）取得最小值-4，结合0＜ω＜3，求出结合ω的值，从而得到函数的解析式．
（2）根据函数y=Asin（ωx+φ）的图象变换规律得出结论．
| 5π |
| 12 |
（2）根据函数y=Asin（ωx+φ）的图象变换规律得出结论．
解答：
（1）解：∵函数f（x）=Asin（ωx+φ）的最小值为-4，可得A=4．
把点P（0，2
）代入f（x）的解析式可得2
=4sinφ，
∴sinφ=
，结合0＜φ＜
，可得φ=
，
∴f（x）=4sin（ωx+
）．
∵当x=-
时，f（x）取得最小值-4，
∴-4=4sin（-ω×
+
），
∴-ω×
+
=2kπ-
，k∈z，∴ω=2-
，结合0＜ω＜3，
可得ω=2，∴f（x）=4sin（2x+
）．
（2）将f（x）=4sin（2x+
）的图象上的每个点的横坐标伸长为原来的两倍，
纵坐标不变，可以得到 f（x）=4sin（x+
）的图象，
再向右平移
个单位，可以得到y=4sinx的图象．
把点P（0，2
| 3 |
| 3 |
∴sinφ=
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
∴f（x）=4sin（ωx+
| π |
| 3 |
∵当x=-
| 5π |
| 12 |
∴-4=4sin（-ω×
| 5π |
| 12 |
| π |
| 3 |
∴-ω×
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 24k |
| 5 |
可得ω=2，∴f（x）=4sin（2x+
| π |
| 3 |
（2）将f（x）=4sin（2x+
| π |
| 3 |
纵坐标不变，可以得到 f（x）=4sin（x+
| π |
| 3 |
再向右平移
| π |
| 3 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
当输入a的值为2，b的值为-3时，右边程序运行的结果是（ ）
| A、-2 | B、-1 | C、1 | D、2 |
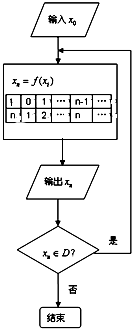对任意函数f（x），其定义域为D，可按如图所示，构造一个数列发生器，要求输入初始数据x0∈D，现定义f（x）=
