题目内容
已知函数f(x)=Asin(ωx+
)(A>0,ω>0)与y=-sinx的图象关于一直线对称.
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短为原来的
倍,纵坐标不变,得到函数y=g(x)的图象.若关于x的方程g(x)+m=0在区间[0,
]上有且只有一个实数解,求实数m的取值范围.
| π |
| 3 |
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)可得两图象的形状和大小完全一样,只是位置不同,比较可得解析式;(Ⅱ)由图象变化法则可得g(x)=sin(2x+
),问题等价于函数g(x)的图象与y=-m只有一个公共点,数形结合可得.
| π |
| 3 |
解答:
 解:(Ⅰ)∵函数f(x)=Asin(ωx+
解:(Ⅰ)∵函数f(x)=Asin(ωx+
)(A>0,ω>0)与y=-sinx的图象关于一直线对称,
∴它们的图象的形状和大小完全一样,只是位置不同,
∴函数y=f(x)的表达式为f(x)=sin(x+
);
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短为原来的
倍,纵坐标不变,得到函数y=g(x)的图象.
∴g(x)=sin(2x+
),可得g(x)在[0,
]单调递增,在[
,
]单调递减,
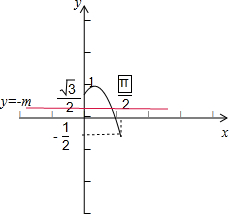
其图象如图所示,
关于x的方程g(x)+m=0在区间[0,
]上有且只有一个实数解,
等价于函数g(x)的图象与y=-m只有一个公共点,
由图象可得-m=1,或-
≤-m<
,
∴实数m的取值范围为:m=-1或-
<m≤
.
 解:(Ⅰ)∵函数f(x)=Asin(ωx+
解:(Ⅰ)∵函数f(x)=Asin(ωx+| π |
| 3 |
∴它们的图象的形状和大小完全一样,只是位置不同,
∴函数y=f(x)的表达式为f(x)=sin(x+
| π |
| 3 |
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短为原来的
| 1 |
| 2 |
∴g(x)=sin(2x+
| π |
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 2 |
其图象如图所示,
关于x的方程g(x)+m=0在区间[0,
| π |
| 2 |
等价于函数g(x)的图象与y=-m只有一个公共点,
由图象可得-m=1,或-
| 1 |
| 2 |
| ||
| 2 |
∴实数m的取值范围为:m=-1或-
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查三角函数的图象和性质,涉及三角函数图象的变换和作图,属中档题.

练习册系列答案
相关题目
如图所示程序运行结果是( )


| A、-8 | B、4 | C、-20 | D、20 |
函数 y=2sin2xcos(π-2x)是( )
A、周期为
| ||
B、周期为
| ||
C、周期为
| ||
D、周期为
|
在如图所示的茎叶图中,甲、乙两组数据的中位数分别是( )


| A、42 42 |
| B、45 46 |
| C、45 42 |
| D、47 48 |
圆x2+y2-4x+6y=0的圆心坐标,半径分别是( )
A、(-2,3),
| ||
B、(2,-3),
| ||
| C、(-2,-3),13 | ||
| D、(2,3),13 |