题目内容
观察下面一组组合数等式:
1•
=n•
;
2•
=n•
;
3•
=n•
…
(Ⅰ)由以上规律,请写出第k(k∈N*)个等式并证明;
(Ⅱ)随机变量X~B(n,p),求证:EX=np.
1•
| C | 1 n |
| C | 0 n-1 |
2•
| C | 2 n |
| C | 1 n-1 |
3•
| C | 3 n |
| C | 2 n-1 |
…
(Ⅰ)由以上规律,请写出第k(k∈N*)个等式并证明;
(Ⅱ)随机变量X~B(n,p),求证:EX=np.
考点:组合及组合数公式,归纳推理
专题:计算题,证明题,规律型
分析:(I)由已知中的式子,分析出第k(k∈N*)个等式为:k•
=n•
,k∈N*,进而根据组合数公式证明可得结论.
(II)将X分解成n个相互独立的,都服从以p为参数的(0-1)分布的随机变量之和:X=X1+X2+…+Xn,Xi~b(1,p),i=1,2,…,n.P{Xi=0}=1-p,P(Xi=1)=p.进而可得结论.
| C | k n |
| C | k-1 n-1 |
(II)将X分解成n个相互独立的,都服从以p为参数的(0-1)分布的随机变量之和:X=X1+X2+…+Xn,Xi~b(1,p),i=1,2,…,n.P{Xi=0}=1-p,P(Xi=1)=p.进而可得结论.
解答:
解:(I)由:
1•
=n•
;
2•
=n•
;
3•
=n•
…
可得第k(k∈N*)个等式为:k•
=n•
,k∈N*,
证明如下:k•
=
=
=n•
证明:(II)将X分解成n个相互独立的,都服从以p为参数的(0-1)分布的随机变量之和:
X=X1+X2+…+Xn,Xi~b(1,p),i=1,2,…,n.
P{Xi=0}=1-p,P(Xi=1)=p.
EXi=0×(1-p)+1×p=p,
E(Xi2)=02×(1-p)+12×p=p,
DXi=E(Xi2)-(EXi)2=p-p2=p(1-p).
EX=EX1+EX2+…+EXn=np,
1•
| C | 1 n |
| C | 0 n-1 |
2•
| C | 2 n |
| C | 1 n-1 |
3•
| C | 3 n |
| C | 2 n-1 |
可得第k(k∈N*)个等式为:k•
| C | k n |
| C | k-1 n-1 |
证明如下:k•
| C | k n |
| kn! |
| k!(n-k)! |
| n(n-1)! |
| (k-1)![(n-1)-(k-1)]! |
| C | k-1 n-1 |
证明:(II)将X分解成n个相互独立的,都服从以p为参数的(0-1)分布的随机变量之和:
X=X1+X2+…+Xn,Xi~b(1,p),i=1,2,…,n.
P{Xi=0}=1-p,P(Xi=1)=p.
EXi=0×(1-p)+1×p=p,
E(Xi2)=02×(1-p)+12×p=p,
DXi=E(Xi2)-(EXi)2=p-p2=p(1-p).
EX=EX1+EX2+…+EXn=np,
点评:本题考查的知识点是归纳推理,组合数公式,随机变量,熟练掌握排列数公式和组合公式,是解答的关键.

练习册系列答案
相关题目
一个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为( )
A、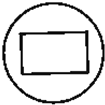 |
B、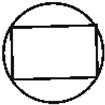 |
C、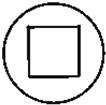 |
D、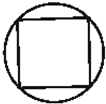 |