题目内容
4.求过(-2,3)点且斜率为2的直线的极坐标方程.分析 由题意知,直线的直角坐标方程为y-3=2(x+2),设M(ρ,θ)为直线上任意一点,将x=ρcos θ,y=ρsin θ代入直角坐标方程即可得出极坐标方程.
解答 解:由题意知,直线的直角坐标方程为y-3=2(x+2),
即2x-y+7=0.
设M(ρ,θ)为直线上任意一点,
将x=ρcos θ,y=ρsin θ代入直角坐标方程2x-y+7=0,
得2ρcos θ-ρsin θ+7=0,这就是所求的极坐标方程.
点评 本题考查了点斜式、直角坐标方程化为极坐标方程,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.函数$f(x)=\left\{\begin{array}{l}-x+3a\\-{(x+1)^2}+2\end{array}\right.$$\begin{array}{l}x<0\\ x≥0\end{array}$,是R上的减函数,则a的取值范围是( )
| A. | (0,1) | B. | $[\frac{1}{3}$,+∞) | C. | (0,$\frac{1}{3}]$ | D. | (0,$\frac{2}{3}]$ |
12.圆ρ=4cosθ的圆心到直线tanθ=1的距离为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
16.一个总体中有600个个体,随机编号为001,002,…,600,利用系统抽样方法抽取容量为24的一个样本,总体分组后在第一组随机抽得的编号为006,则在编号为051~125之间抽得的编号为( )
| A. | 056,080,104 | B. | 054,078,102 | C. | 054,079,104 | D. | 056,081,106 |
14.在极坐标系中,曲线C:sinθ=|cosθ|上不同的两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,则|MN|=( )
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |
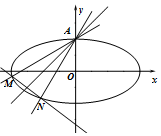 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.