题目内容
14.在极坐标系中,曲线C:sinθ=|cosθ|上不同的两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,则|MN|=( )| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |
分析 曲线C转化为y=|x|,直线l转化为:x-2y-2=0,由两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,求出m=3,联立$\left\{\begin{array}{l}{x-2y+3=0}\\{y=|x|}\end{array}\right.$,能求出|MN|.
解答 解:∵曲线C:sinθ=|cosθ|,
∴ρsinθ=|ρcosθ|,∴y=|x|,
∵直线l:ρcosθ-2ρsinθ=2,
∴直线l:x-2y-2=0,
d=$\frac{|m+2|}{\sqrt{5}}$=$\sqrt{5}$,∴|m+2|=5,解得m=3或m=-7(舍),
联立$\left\{\begin{array}{l}{x-2y+3=0}\\{y=|x|}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴M(-1,1),N(3,3),
∴|MN|=$\sqrt{(3-1)^{2}+(3+1)^{2}}$=2$\sqrt{5}$.
故选:A.
点评 本题考查两点间距离的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体中最长的棱长为( )
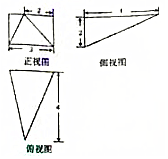

| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
3.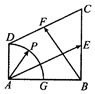 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |