题目内容
设变量x,y满足约束条件
,则目标函数z=
的最大值为 .
|
| y |
| x+2 |
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:由约束条件作出可行域,把目标函数z=
化为z=
,其几何意义是可行域内的动点与定点M(-2,0)连线的斜率,数形结合得到使z=
最大的点,联立方程组求出点的坐标,代入目标函数得答案.
| y |
| x+2 |
| y-0 |
| x-(-2) |
| y |
| x+2 |
解答:
解:由约束条件
作出可行域如图,

联立
,解得A(
,
).
联立
,解得B(2,3).
的几何意义是可行域内的动点与定点M(-2,0)连线的斜率.
∴目标函数z=
的最大值为
=
.
故答案为:
.
|

联立
|
| 2 |
| 3 |
| 1 |
| 3 |
联立
|
| y |
| x+2 |
∴目标函数z=
| y |
| x+2 |
| 3-0 |
| 2-(-2) |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
在△ABC中,a2+b2-
ab=c2,则角C=( )
| 3 |
| A、30° | B、60° |
| C、150° | D、45°或35° |
在△ABC中,D是AB中点,E是AC中点,CD与BE交于点F,设
=
,
=
,
=x
+y
则(x,y)为( )
| AB |
| a |
| AC |
| b |
| AF |
| a |
| b |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
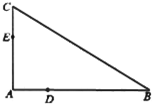 如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.