题目内容
 如图,三棱柱ABC-A1B1C1的底面是边长2的正三角形,侧棱与底面垂直,且长为
如图,三棱柱ABC-A1B1C1的底面是边长2的正三角形,侧棱与底面垂直,且长为| 3 |
(1)求证:B1C∥平面A1BD;
(2)求点A到平面A1BD的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连结DM,证明MD∥B1C,即可证明B1C∥平面A1BD;
(2)利用VA1-BDA=VA-A1BD,求点A到平面A1BD的距离.
(2)利用VA1-BDA=VA-A1BD,求点A到平面A1BD的距离.
解答:
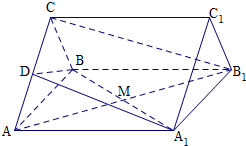 (1)证明:连结DM,
(1)证明:连结DM,
∵三棱柱ABC-A1B1C1的侧棱与底面垂直,
∴四边形AA1B1B是矩形,
∴M为A1B的中点.
∵D是AC的中点,∴MD是三角形AB1C的中位线,
∴MD∥B1C.
∵MD?平面A1BD,B1C?平面A1BD,
∴B1C∥平面A1BD.
(2)解:设点A到平面A1BD的距离为h,
∵AA1⊥平面ABC,BD=
,
∴A1D=2,A1B=
,
∴A1D⊥BD,
∴S△A1BD=
BD•A1D=
,
由VA1-BDA=VA-A1BD得h=
=
.
 (1)证明:连结DM,
(1)证明:连结DM,∵三棱柱ABC-A1B1C1的侧棱与底面垂直,
∴四边形AA1B1B是矩形,
∴M为A1B的中点.
∵D是AC的中点,∴MD是三角形AB1C的中位线,
∴MD∥B1C.
∵MD?平面A1BD,B1C?平面A1BD,
∴B1C∥平面A1BD.
(2)解:设点A到平面A1BD的距离为h,
∵AA1⊥平面ABC,BD=
| 3 |
∴A1D=2,A1B=
| 7 |
∴A1D⊥BD,
∴S△A1BD=
| 1 |
| 2 |
| 3 |
由VA1-BDA=VA-A1BD得h=
| ||||||
|
| ||
| 2 |
点评:此题重点考查了线面平行的判定定理,考查了点A到平面A1BD的距离,及学生的空间想象能力及计算能力.

练习册系列答案
相关题目
某学校实行改革,每天上午改为上五节课,40分钟一节,其中高二(12)班周二上午安排数学、物理、生物、语文、体育五节课,若体育课不排第一节,数学课与物理课不相邻的排法总数为( )
| A、48 | B、60 | C、72 | D、96 |
在空间直角坐标系中,定义:平面α的一般方程为:Ax+By+Cz+D=0(A,B,C,D∈R,且A,B,C不同时为零),点P(x0,y0,z0)到平面α的距离为:d=
,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
| |Ax0+By0+Cz0+D| | ||
|
A、
| ||||
B、
| ||||
| C、2 | ||||
| D、5 |
| ∫ |
0 |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
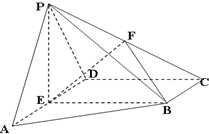 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.