题目内容
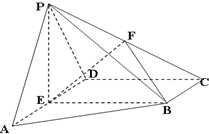 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.(Ⅰ)求证AD⊥平面PBE;
(Ⅱ)求证PA∥平面BEF;
(Ⅲ)若PB=AD,求二面角F-BE-C的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明AD⊥平面PBE,只需证明BE⊥AD,PE⊥AD;
(Ⅱ)证明PA∥平面BEF,只需证明FG∥PA;
(Ⅲ)取CD中点H,连接FH,GH,可知∠FGH为二面角F-BE-C的平面角,即可求二面角F-BE-C的大小.
(Ⅱ)证明PA∥平面BEF,只需证明FG∥PA;
(Ⅲ)取CD中点H,连接FH,GH,可知∠FGH为二面角F-BE-C的平面角,即可求二面角F-BE-C的大小.
解答:
(Ⅰ)证明:由已知得ED∥BC,ED=BC,
故BCDE是平行四边形,所以BE∥CD,BE=CD,
因为AD⊥CD,所以BE⊥AD,
由PA=PD及E是AD的中点,得PE⊥AD,
又因为BE∩PE=E,所以AD⊥平面PBE.
(Ⅱ)证明:连接AC交EB于G,再连接FG,
由E是AD的中点及BE∥CD,知G是BF的中点,
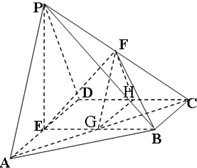
又F是PC的中点,故FG∥PA,
又因为FG?平面BEF,PA?平面BEF,
所以PA∥平面BEF.
(Ⅲ)解:设PA=PD=AD=2BC=2CD=2a,
则PF=
a,又PB=AD=2a,EB=CD=a,
故PB2=PE2+BE2即PE⊥BE,
又因为BE⊥AD,AD∩PE=E,
所以BE⊥平面PAD,得BE⊥PA,故BE⊥FG,
取CD中点H,连接FH,GH,可知GH∥AD,因此GH⊥BE,
综上可知∠FGH为二面角F-BE-C的平面角.
可知FG=
PA=a,FH=
PD=a,GH=
AD=a,
故∠FGH=60°,所以二面角F-BE-C等于60°.
故BCDE是平行四边形,所以BE∥CD,BE=CD,
因为AD⊥CD,所以BE⊥AD,
由PA=PD及E是AD的中点,得PE⊥AD,
又因为BE∩PE=E,所以AD⊥平面PBE.
(Ⅱ)证明:连接AC交EB于G,再连接FG,
由E是AD的中点及BE∥CD,知G是BF的中点,

又F是PC的中点,故FG∥PA,
又因为FG?平面BEF,PA?平面BEF,
所以PA∥平面BEF.
(Ⅲ)解:设PA=PD=AD=2BC=2CD=2a,
则PF=
| 3 |
故PB2=PE2+BE2即PE⊥BE,
又因为BE⊥AD,AD∩PE=E,
所以BE⊥平面PAD,得BE⊥PA,故BE⊥FG,
取CD中点H,连接FH,GH,可知GH∥AD,因此GH⊥BE,
综上可知∠FGH为二面角F-BE-C的平面角.
可知FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故∠FGH=60°,所以二面角F-BE-C等于60°.
点评:本题考查线面垂直、线面平行,考查面面角,解题的关键是掌握线面垂直、线面平行的判定方法,正确找出面面角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
,
满足
•
=0,|
|=1,|
|=2,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
若函数f(x)=x3+x2+mx+1是R上的单调增函数,则实数m的取值范围是( )
A、[
| ||
B、(-
| ||
C、(-∞,
| ||
D、(-∞,
|
 如图,三棱柱ABC-A1B1C1的底面是边长2的正三角形,侧棱与底面垂直,且长为
如图,三棱柱ABC-A1B1C1的底面是边长2的正三角形,侧棱与底面垂直,且长为