题目内容
 如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=| 2 |
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面BCE;
( III)求三棱锥F-ADB的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)取BE的中点G,利用GF为三角形BCE的中位线,证明四边形GFAD为平行四边形,从而证明AF∥平面BDE.
(Ⅱ)先证AF⊥平面BCE,由AF∥GD可得GD⊥平面BCE,进而证明平面BDE⊥平面BCE.
(Ⅲ)由AB2+AC2=BC2,得AF=
BC=
,由AD⊥平面ABC,四边形GFAD为平行四边形,得四边形GFAD为矩形,由AD⊥平面ABC,AF⊥平面BCE,得BF⊥平面GFAD,由VF-ADB=
VB-ADGF,利用等积法能求出三棱锥F-ADB的体积.
(Ⅱ)先证AF⊥平面BCE,由AF∥GD可得GD⊥平面BCE,进而证明平面BDE⊥平面BCE.
(Ⅲ)由AB2+AC2=BC2,得AF=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:
(本小题满分12分)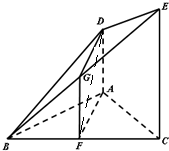
(Ⅰ)证明:取BE的中点G,连接GF,GD,
∵AD⊥平面ABC,CE⊥平面ABC,
∴AD∥EC,且平面ABC⊥平面ACED,
∵GF为△BCE的中位线,
∴GF∥EC∥DA,GF=
CE=DA,
∴四边形GFAD为平行四边形,
∴AF∥GD,又GD?平面BDE,
∴AF∥平面BDE.(4分)
(Ⅱ)证明:∵AB=AC,F为BC的中点,∴AF⊥BC,
又CE⊥平面ABC,AF?平面ABC,∴AF⊥EC,
又BC∩EC=C,∴AF⊥平面BCE,
∵AF∥GD,∴GD⊥平面BCE,
又GD?平面BDE,∴平面BDE⊥平面BCE.(8分)
(Ⅲ)解:∵AC=AD=AB=1,BC=
,CE=2,F为BC的中点,
∴AB2+AC2=BC2,
∴AF=
BC=
,
∵AD⊥平面ABC,四边形GFAD为平行四边形,
∴四边形GFAD为矩形,
∴S矩形GFAD=AF×AD=
×1=
,
∵AD⊥平面ABC,AF⊥平面BCE,∴BF⊥平面GFAD,
连结DF,三棱锥F-ADB的体积:
VF-ADB=
VB-ADGF=
×S矩形GFAD×BF=
×
×
=
.(12分)

(Ⅰ)证明:取BE的中点G,连接GF,GD,
∵AD⊥平面ABC,CE⊥平面ABC,
∴AD∥EC,且平面ABC⊥平面ACED,
∵GF为△BCE的中位线,
∴GF∥EC∥DA,GF=
| 1 |
| 2 |
∴四边形GFAD为平行四边形,
∴AF∥GD,又GD?平面BDE,
∴AF∥平面BDE.(4分)
(Ⅱ)证明:∵AB=AC,F为BC的中点,∴AF⊥BC,
又CE⊥平面ABC,AF?平面ABC,∴AF⊥EC,
又BC∩EC=C,∴AF⊥平面BCE,
∵AF∥GD,∴GD⊥平面BCE,
又GD?平面BDE,∴平面BDE⊥平面BCE.(8分)
(Ⅲ)解:∵AC=AD=AB=1,BC=
| 2 |
∴AB2+AC2=BC2,
∴AF=
| 1 |
| 2 |
| ||
| 2 |
∵AD⊥平面ABC,四边形GFAD为平行四边形,
∴四边形GFAD为矩形,
∴S矩形GFAD=AF×AD=
| ||
| 2 |
| ||
| 2 |
∵AD⊥平面ABC,AF⊥平面BCE,∴BF⊥平面GFAD,
连结DF,三棱锥F-ADB的体积:
VF-ADB=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 12 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
双曲线
-y2=1的渐近线方程为( )
| x2 |
| 2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
三棱锥S-ABC的顶点都在同一球面上,且SA=AC=SB=BC=
,SC=2,则该球的体积为( )
| 2 |
A、
| ||
B、
| ||
| C、2π | ||
| D、8π |
已知正项数列{an}的前n项和为Sn,且2Sn=an+
,则S2015的值是( )
| 1 |
| an |
A、2015+
| ||||
B、2015-
| ||||
| C、2015 | ||||
D、
|
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标,若方程x4+ax-4=0各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是( )
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
| A、(-∞,-3) |
| B、(-3,3) |
| C、(3,∞) |
| D、(-∞,-6)∪(6,∞) |