题目内容
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标,若方程x4+ax-4=0各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是( )
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
| A、(-∞,-3) |
| B、(-3,3) |
| C、(3,∞) |
| D、(-∞,-6)∪(6,∞) |
考点:函数的图象,二元一次不等式(组)与平面区域
专题:函数的性质及应用
分析:原方程等价于x3+a=
,分别作出y=x3+a与y=
的图象:分a>0与a<0讨论,利用数形结合即可得到结论.
| 4 |
| x |
| 4 |
| x |
解答:
解:方程的根显然x≠0,原方程x4+ax-4=0,等价为方程x3+a=
,
原方程的实根是曲线y=x3+a与曲线y=
的交点的横坐标;
曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的.
若交点(xi,
)(i=1,2,k)均在直线y=x的同侧,因直线y=x与y=
交点为:(-2,-2),(2,2);
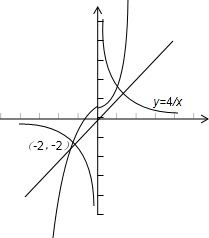
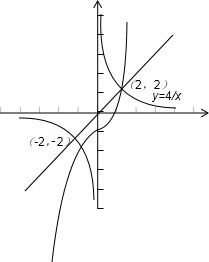
所以结合图象可得:
或
,
解得a>6或a<-6,即实数a的取值范围是(-∞,-6)∪(6,∞),
故选:D
| 4 |
| x |
原方程的实根是曲线y=x3+a与曲线y=
| 4 |
| x |
曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的.
若交点(xi,
| 4 |
| xi |
| 4 |
| x |


所以结合图象可得:
|
|
解得a>6或a<-6,即实数a的取值范围是(-∞,-6)∪(6,∞),
故选:D
点评:本题考查函数与方程的综合运用,利用数形结合是解决本题的关键.注意合理地进行等价转化.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=