题目内容
已知正项数列{an}的前n项和为Sn,且2Sn=an+
,则S2015的值是( )
| 1 |
| an |
A、2015+
| ||||
B、2015-
| ||||
| C、2015 | ||||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:2Sn=an+
,可得2a1=a1+
,解得a1=1.同理解得a2=
-1,a3=
-
.…,猜想an=
-
..验证满足条件,进而得出.
| 1 |
| an |
| 1 |
| a1 |
| 2 |
| 3 |
| 2 |
| n |
| n-1 |
解答:
解:∵2Sn=an+
,∴2a1=a1+
,解得a1=1.
当n=2时,2(1+a2)=a2+
,化为
+2a2-1=0,又a2>0,解得a2=
-1,
同理可得a3=
-
.
猜想an=
-
.
验证:2Sn=2[(1-0)+(
-1)+…+(
-
)]=2
,an+
=
-
+
=2
,
因此满足2Sn=an+
,
∴an=
-
.
∴Sn=
.
∴S2015=
.
故选:D.
| 1 |
| an |
| 1 |
| a1 |
当n=2时,2(1+a2)=a2+
| 1 |
| a2 |
| a | 2 2 |
| 2 |
同理可得a3=
| 3 |
| 2 |
猜想an=
| n |
| n-1 |
验证:2Sn=2[(1-0)+(
| 2 |
| n |
| n-1 |
| n |
| 1 |
| an |
| n |
| n-1 |
| 1 | ||||
|
| n |
因此满足2Sn=an+
| 1 |
| an |
∴an=
| n |
| n-1 |
∴Sn=
| n |
∴S2015=
| 2015 |
故选:D.
点评:本题考查了猜想分析归纳得出数列的通项公式的方法、递推式的应用,考查了由特殊到一般的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={1,2,3,4,5},B={1,3,5},则∁AB=( )
| A、{1,3,5} |
| B、{2,4} |
| C、{1,2,3,4,5} |
| D、∅ |
下列命题中,错误的是( )
| A、平行于同一平面的两个平面平行 |
| B、垂直于同一个平面的两个平面平行 |
| C、若a,b是异面直线,则经过直线a与直线b平行的平面有且只有一个 |
| D、若一个平面与两个平行平面相交,则交线平行 |
 如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,凸多面体ABCED中,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=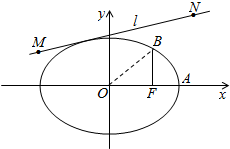 如图,已知椭圆C的中心在原点,焦点在x轴上,离心率e=
如图,已知椭圆C的中心在原点,焦点在x轴上,离心率e=