题目内容
三棱锥S-ABC的顶点都在同一球面上，且SA=AC=SB=BC=
，SC=2，则该球的体积为（ ）
| 2 |
A、
| ||
B、
| ||
| C、2π | ||
| D、8π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：由勾股定理的逆定理可得SA⊥AC，SB⊥BC，取SC的中点O，连接OA，OB，则由直角三角形的斜边上的中线即为斜边的一半，即有球的半径r为1，运用球的体积公式计算即可得到．
解答：
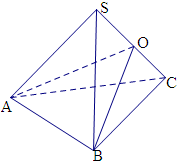解：由于SA=AC=SB=BC=
，SC=2，
则SA2+AC2=SC2，SB2+BC2=SC2，
即有SA⊥AC，SB⊥BC，
取SC的中点O，连接OA，OB，
则由直角三角形的斜边上的中线即为斜边的一半，
可得OA=OB=OC=OS=1，
即有球的半径r为1，
则球的体积为
πr3=
．
故选B．
解：由于SA=AC=SB=BC=| 2 |
则SA2+AC2=SC2，SB2+BC2=SC2，
即有SA⊥AC，SB⊥BC，
取SC的中点O，连接OA，OB，
则由直角三角形的斜边上的中线即为斜边的一半，
可得OA=OB=OC=OS=1，
即有球的半径r为1，
则球的体积为
| 4 |
| 3 |
| 4π |
| 3 |
故选B．
点评：本题考查球的体积的求法，解题的关键是求出球的半径，同时考查直角三角形的性质以及勾股定理的逆定理，考查运算能力，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图所示，凸多面体ABCED中，AD⊥平面ABC，CE⊥平面ABC，AC=AD=AB=1，BC=设函数f（x）=ax+xa（a＞0），则下列说法正确的是（ ）
| A、?a＞0，f（x）为偶函数，且在R上单调递增 |
| B、?a＞0，f（x）-1为奇函数，且在R上单调递增 |
| C、?a＞0，f（x）为奇函数，且在R上单调递减 |
| D、?a＞0，f（x）-1为偶函数，且在R上单调递减 |
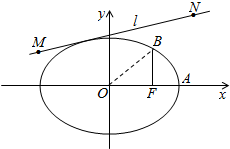如图，已知椭圆C的中心在原点，焦点在x轴上，离心率e=