题目内容
在矩形ABCD中，对角线AC与相邻两边所成的角为α，β，则有cos2α+cos2β=1．
类比到空间中的一个正确命题是：在长方体ABCDA1B1C1D1中，对角线AC1与相邻三个面所成的角为α，β，γ，则cos2α+cos2β+cos2γ= ．
类比到空间中的一个正确命题是：在长方体ABCDA1B1C1D1中，对角线AC1与相邻三个面所成的角为α，β，γ，则cos2α+cos2β+cos2γ=
考点：类比推理,棱柱的结构特征
专题：空间位置关系与距离
分析：由类比规则，点类比线，线类比面，可得出在长方体ABCDA1B1C1D1中，对角线AC1与相邻三个面所成的角为α，β，γ，则cos2α+cos2β+cos2γ=2，解直角三角形证明其为真命题即可．
解答：
解：我们将平面中的两维性质，类比推断到空间中的三维性质．
由在长方形中，设一条对角线与其一顶点出发的两条边所成的角分别是α，β，
则有cos2α+cos2β=1，
我们根据长方体性质可以类比推断出空间性质，
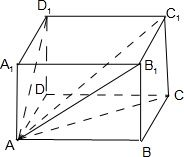
∵长方体ABCD-A1B1C1D1中，如图
对角线AC1与过A点的三个面ABCD，AA1B1B、AA1D1D所成的角分别为α，β，γ，
∴cosα=
，cosβ=
，cosγ=
，
∴cos2α+cos2β+cos2γ=
，
令同一顶点出发的三个棱的长分别为a，b，c，则有cos2α+cos2β+cos2γ=
=
=2
故答案为：cos2α+cos2β+cos2γ=2．
解：我们将平面中的两维性质，类比推断到空间中的三维性质．由在长方形中，设一条对角线与其一顶点出发的两条边所成的角分别是α，β，
则有cos2α+cos2β=1，
我们根据长方体性质可以类比推断出空间性质，
∵长方体ABCD-A1B1C1D1中，如图
对角线AC1与过A点的三个面ABCD，AA1B1B、AA1D1D所成的角分别为α，β，γ，
∴cosα=
| AC |
| AC1 |
| AB1 |
| AC1 |
| AD1 |
| AC1 |
∴cos2α+cos2β+cos2γ=
| AC2+AB1 2+AD1 2 |
| AC1 2 |
令同一顶点出发的三个棱的长分别为a，b，c，则有cos2α+cos2β+cos2γ=
| AC2+AB1 2+AD1 2 |
| AC1 2 |
| a2+b2+a2+c2+b2+c2 |
| a2+b2+c2 |
故答案为：cos2α+cos2β+cos2γ=2．
点评：本题考查类比推理及棱柱的结构特征，线面角的定义，综合性强是一个常考的题型．
练习册系列答案
相关题目
已知点P（m，n）是直线2x+y+5=0上的任意一点，则m2+n2的最小值为（ ）
A、
| ||
B、
| ||
| C、5 | ||
| D、10 |
设抛物线C1：y2=2x与双曲线C2：
-
=1的焦点重合，且双曲线C2的渐近线为y=±
x，则双曲线C2的实轴长为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
如图所示，凸多面体ABCED中，AD⊥平面ABC，CE⊥平面ABC，AC=AD=AB=1，BC=设函数f（x）=ax+xa（a＞0），则下列说法正确的是（ ）
| A、?a＞0，f（x）为偶函数，且在R上单调递增 |
| B、?a＞0，f（x）-1为奇函数，且在R上单调递增 |
| C、?a＞0，f（x）为奇函数，且在R上单调递减 |
| D、?a＞0，f（x）-1为偶函数，且在R上单调递减 |