题目内容
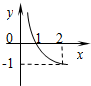 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )| A、g(x)=2x | ||
B、g(x)=(
| ||
C、g(x)=log
| ||
| D、g(x)=log2x |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:f(x)=logax(a>0,且a≠1)与g(x)=ax(a>0且,a≠1)互为反函数,再根据单调性可判断a的范围.
解答:
解:∵根据f(x)=logax(a>0,且a≠1)的图象可知0<a<1,
与g(x)=ax(a>0且,a≠1)互为反函数,
∴g(x)=ax(0<a<1)
故选:B
与g(x)=ax(a>0且,a≠1)互为反函数,
∴g(x)=ax(0<a<1)
故选:B
点评:本题考查了指数函数,对数函数的图象和性质,难度不大,运用这个知识点即可求解,得出答案.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln 2+
| ||
B、ln 2-
| ||
C、ln 2-
| ||
D、ln 2-
|
点A(2,0),B(4,2),若|
|=2|
|,则点C坐标为( )
| AB |
| AC |
| A、(1,-1) |
| B、(1,-1)或(5,-1) |
| C、(1,-1)或(3,1) |
| D、无数多个 |
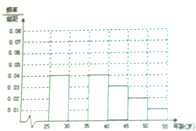 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.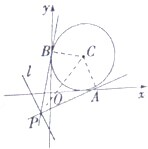 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.