题目内容

已知x＞1，y＞2，x+y=15，则函数z=（x-1）（y-2）的最大值为
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：由题意结合基本不等式可得z=（x-1）（y-2）≤(
x-1+y-2
2
)2，代值计算可得．
解答： 解：∵x＞1，y＞2，
∴x-1＞0，y-2＞0，
∴z=（x-1）（y-2）≤(
x-1+y-2
2
)2
∵x+y=15，∴(
x-1+y-2
2
)2=36
当且仅当x-1=y-2即x=7且y=8是取最大值36，
故答案为：36
点评：本题考查基本不等式，属基础题．
练习册系列答案
相关题目
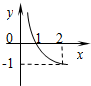已知函数f（x）=logax（a＞0，且a≠1）的图象如图所示，函数y=g（x）是函数y=f（x）的反函数，则函数y=g（x）的解析式为（　　）
A、g（x）=2x
B、g(x)=(
1
2
)x
C、g(x)=log
1
2
x
D、g（x）=log2x
若a，b∈R，则下列命题正确的是（　　）
A、若a＞b，则a2＞b2
B、若a＞b，则
1
a
＞
1
b
C、若a＞|b|，则a2＞b2
D、若ac＞bc，则a＞b
函数y=
3
4
x4-x3的极值点的个数为（　　）
A、0个B、1个C、2个D、3个
关于函数f（x）=4sin（2x+
π
3
），（x∈R）有下列命题：
①y=f（x）是以2π为最小正周期的周期函数； 
②y=f（x）可改写为y=4cos（2x-
π
6
）；
③y=f（x）的图象关于点（-
π
6
，0）对称；   
④y=f（x）的图象关于直线x=-
5π
12
对称；
⑤y=|f（x）|是以π为最小正周期的周期函数．
其中正确的序号为
 
．
已知函数f（x）=
ax
x2-1
（a＞0）．
（1）判断并证明函数f（x）的奇偶性；
（2）判断函数f（x）的单调性，并用函数的单调性定义给予证明．
已知函数f（x）=5sinxcosx-5
3
cos2x+
5
3
2
．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）的单调递增区间，并求出f（x）在[
π
3
，
5π
6
]上的最大值与最小值．
设函数f（x）=sinx+cosx．
（Ⅰ）求函数g（x）=f（x）•f′（x）+[f（x）]2的周期和对称轴；
（Ⅱ）若h（x）=（f（x）-sinx）cos（x-
π
3
），求使h（x）＞
1+
3
4
成立的x的取值集合．
定义◇的运算为a◇b=
ba≥b
ab＞a
，则f（x）=3x◇3-x的值域为（　　）
A、（0，1]
B、[1，+∞）
C、（0，+∞）
D、（-∞，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网