题目内容
过原点O的圆C,与x轴相交于点A(4,0),与y轴相交于点B(0,2).
(1)求圆C的标准方程;
(2)直线l过B点与圆C相切,求直线L的方程,并化为一般式.
(1)求圆C的标准方程;
(2)直线l过B点与圆C相切,求直线L的方程,并化为一般式.
考点:圆的标准方程,圆的切线方程
专题:计算题,直线与圆
分析:(1)设圆C的标准方程为:(x-a)2+(y-b)2=r2,则分别代入原点和A(4,0),B(0,2)得到方程组,解出即可得到;
(2)由(1)得到圆心C为(2,1),半径r=
,由于直线l过B点与圆C相切,则设直线l:x=0或y=kx+2,分别考虑运用直线与圆相切的条件:d=r,解方程即可得到所求直线方程.
(2)由(1)得到圆心C为(2,1),半径r=
| 5 |
解答:
解:(1)设圆C的标准方程为:(x-a)2+(y-b)2=r2,
则分别代入原点和A(4,0),B(0,2)得到,
,解得
,
则圆C的标准方程为:(x-2)2+(y-1)2=5;
(2)由(1)得到圆心C为(2,1),半径r=
,
由于直线l过B点与圆C相切,
则设直线l:x=0或y=kx+2,
当l:x=0时,C到l的距离为2,不合题意,舍去;
当l:y=kx+2,由直线与圆相切,得到d=r,
即有
=
,解得k=2,
故直线l:y=2x+2,即为2x-y+2=0.
则分别代入原点和A(4,0),B(0,2)得到,
|
|
则圆C的标准方程为:(x-2)2+(y-1)2=5;
(2)由(1)得到圆心C为(2,1),半径r=
| 5 |
由于直线l过B点与圆C相切,
则设直线l:x=0或y=kx+2,
当l:x=0时,C到l的距离为2,不合题意,舍去;
当l:y=kx+2,由直线与圆相切,得到d=r,
即有
| |2k-1+2| | ||
|
| 5 |
故直线l:y=2x+2,即为2x-y+2=0.
点评:本题考查直线与圆的位置关系,考查圆的方程的求法和直线与圆相切的条件,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则AF:FB=( )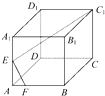

| A、1:1 | B、1:2 |
| C、1:3 | D、1:4 |
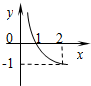 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )| A、g(x)=2x | ||
B、g(x)=(
| ||
C、g(x)=log
| ||
| D、g(x)=log2x |
函数y=
x4-x3的极值点的个数为( )
| 3 |
| 4 |
| A、0个 | B、1个 | C、2个 | D、3个 |
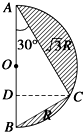 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为