题目内容
一名篮球运动员在比赛时罚球命中率为50%，则他在5次罚球中罚失2次的概率是 ．
考点：n次独立重复试验中恰好发生k次的概率
专题：概率与统计
分析：由条件根据相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式，求得结果．
解答：
解：由题意可得，他在5次罚球中罚失2次的概率是
•0.53•0.52=
，
故答案为：
．
| C | 3 5 |
| 5 |
| 32 |
故答案为：
| 5 |
| 16 |
点评：本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式的应用，属于基础题．
练习册系列答案
相关题目
关于空间两条直线a、b和平面α，下列命题正确的是（ ）
| A、若a∥b，b?α，则a∥α |
| B、若a∥α，b?α，则a∥b |
| C、若a⊥α，b⊥α，则a∥b |
| D、若a∥α，b∥α，则a∥b |
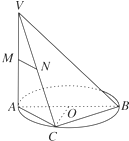如图，AB是⊙O的直径，VA垂直⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（ ）| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
已知圆的方程为x2+y2-2xlga+2ylg（10a）+2lg2a+2lga=0（a＞0），则圆心所在的直线方程为（ ）
| A、x-y+1=0 |
| B、x+y+1=0 |
| C、x-y-1=0 |
| D、x+y-1=0 |