题目内容
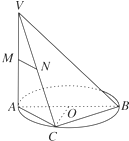如图，AB是⊙O的直径，VA垂直⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（ ）| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：由已知得AC⊥BC，VA⊥BC，由此得平面VAC⊥平面VBC，OC与AC不垂直，从而OC⊥平面VAC不成立，由M，N分别为VA，VC的中点，得MN与BC所成的角为90°，MN∥AB不成立．
解答：
解：∵AB是⊙O的直径，点C是圆周上不同于A，B的任意一点，
∴AC⊥BC，
∵VA垂直⊙O所在的平面，BC?⊙O所在的平面，
∴VA⊥BC，
又AC∩VA=A，∴BC⊥平面VAC，
又BC?平面VBC，∴平面VAC⊥平面VBC，故A正确；
∵AB是⊙O的直径，点C是圆周上不同于A，B的任意一点，
∴AC⊥BC，又A、B、C、O共面，∴OC与AC不垂直，
∴OC⊥平面VAC不成立，故B不正确；
∵M，N分别为VA，VC的中点，
∴MN∥AC，又AC⊥BC，∴MN与BC所成的角为90°，故C不正确；
∵MN∥AC，AC∩AB=A，∴MN∥AB不成立，故D不正确．
故选：A．
∴AC⊥BC，
∵VA垂直⊙O所在的平面，BC?⊙O所在的平面，
∴VA⊥BC，
又AC∩VA=A，∴BC⊥平面VAC，
又BC?平面VBC，∴平面VAC⊥平面VBC，故A正确；
∵AB是⊙O的直径，点C是圆周上不同于A，B的任意一点，
∴AC⊥BC，又A、B、C、O共面，∴OC与AC不垂直，
∴OC⊥平面VAC不成立，故B不正确；
∵M，N分别为VA，VC的中点，
∴MN∥AC，又AC⊥BC，∴MN与BC所成的角为90°，故C不正确；
∵MN∥AC，AC∩AB=A，∴MN∥AB不成立，故D不正确．
故选：A．
点评：本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
下列有关命题的叙述错误的是（ ）
| A、对于命题P：?x∈R，x2+x-1＜0，则￢P为：?x∈R，x2+x-1≥0 |
| B、若“P且Q”为假命题，则P，Q均为假命题 |
| C、“x＞2”是“x2-3x+2＞0”的充分不必要条件 |
| D、命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0” |
已知向量
=（2，3），
=（6，x），且
⊥
，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、4 | B、-4 | C、-9 | D、9 |
下列结论错误的是（ ）
A、若ab＞0，则
| ||||
B、函数y=cosx+
| ||||
| C、函数y=2x+2-x的最小值为2 | ||||
D、若x∈（0，1），则函数y=lnx+
|
下列说法中，正确的是（ ）
| A、棱柱的侧面可以是三角形 |
| B、有两个面平行，其余各面都是四边形的几何体叫棱柱 |
| C、将直角三角形绕它的一边所在的直线旋转一周，形成的几何体一定是圆锥 |
| D、棱台的侧棱所在的直线交于一点 |