题目内容
14.设P是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上的一点,F1,F2是该椭圆的两个焦点,且∠F1PF2=$\frac{π}{3}$,则△F1PF2的面积为3$\sqrt{3}$,△F1PF2内切圆半径为$\frac{\sqrt{3}}{3}$.分析 先根据椭圆的方程求得c,进而求得|F1F2|,设出|PF1|=t1,|PF2|=t2,利用余弦定理可求得t1t2的值,最后利用三角形面积公式求解.由S=$\frac{1}{2}(a+b+c)r$,能求出△F1PF2内切圆半径.
解答 解:∵a=5,b=3,∴c=4,即|F1F2|=8.
设|PF1|=t1,|PF2|=t2,
则根据椭圆的定义可得:t1+t2=10①,
在△F1PF2中∠F1PF2=60°,
∴根据余弦定理可得:t12+t22-2t1t2•cos60°=82②,
由①2-②得t1•t2=12,
∴由正弦定理可得:S△F1PF2=$\frac{1}{2}$t1t2•sin60°=$\frac{1}{2}$×12×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
∴△F1PF2的面积3$\sqrt{3}$.
设△F1PF2内切圆半径为r,
∵△F1PF2的周长为L=10+8=18,面积为S=$3\sqrt{3}$,
∴r=$\frac{S}{\frac{1}{2}L}$=$\frac{3\sqrt{3}}{9}$=$\frac{\sqrt{3}}{3}$.
故答案为:3$\sqrt{3}$,$\frac{\sqrt{3}}{3}$.
点评 解决此类问题的关键是熟练掌握椭圆的标准方程、椭圆的简单性质,以及熟练掌握解三角形的有关知识.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
4.函数$y=\frac{1}{lg(x-1)}$的定义域为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (1,2)∪(2,+∞) | D. | (1,3)∪(3,+∞) |
9.若l,m,n是不相同的空间直线,α,β是不重合的两个平面,则下列命题正确的是( )
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
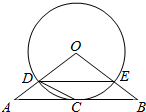 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.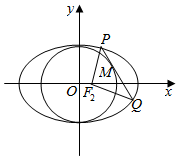 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上