题目内容
5．函数g（x）是函数f（x）=loga（x-2）（a＞0，且a≠1）的反函数，则函数g（x）的图象过定点（0，3）．分析 函数f（x）=loga（x-2）（a＞0，且a≠1）的图象经过定点（3，0），利用互为反函数的性质即可得出．
解答 解：函数f（x）=loga（x-2）（a＞0，且a≠1）的图象经过定点（3，0），
∵函数g（x）是函数f（x）=loga（x-2）（a＞0，且a≠1）的反函数，
则函数g（x）的图象过定点（0，3），
故答案为：（0，3）．
点评 本题考查了互为反函数的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16．过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$中心的直线交椭圆于A，B两点，右焦点为F2（c，0），则△ABF2的最大面积为（ ）
| A． | b2 | B． | ab | C． | ac | D． | bc |
13．已知函数$f（x）=1-2{cos^2}（x+\frac{π}{4}）$，下列说法正确的是（ ）
| A． | f（x）是最小正周期为π的奇函数 | B． | f（x）是最小正周期为π的偶函数 | ||
| C． | f（x）是最小正周期为$\frac{π}{2}$的偶函数 | D． | f（x）是最小正周期为$\frac{π}{2}$的奇函数 |
10．已知圆M：（x+$\sqrt{7}$）2+y2=64，定点N（$\sqrt{7}$，0），点P为圆M上的动点，点Q在NP上，点G 在线段MP上，且满足$\overrightarrow{NP}$=2$\overrightarrow{NQ}$，$\overrightarrow{GQ}$•$\overrightarrow{NP}$=0，则点G的轨迹方程是（ ）
| A． | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B． | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D． | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
17．若圆x2+y2+2x-4y=0关于直线3x+y+m=0对称，则实数m的值为（ ）
| A． | -3 | B． | -1 | C． | 1 | D． | 3 |
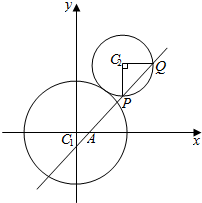已知圆C1：x2+y2=9与圆C2：（x-3）2+（y-4）2=r2（r＞0）相外切．