题目内容
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
分析 设数列{an}的前n项和为Sn,根据a1=1,(n+1)an+1=2(a1+a2+…+an)=2Sn(n∈N+),可得a2=1,当n≥2时,可得2an=(n+1)an+1-nan,化为:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+2}{n+1}$.再利用“累乘求积”方法即可得出.
解答 解:设数列{an}的前n项和为Sn,∵a1=1,(n+1)an+1=2(a1+a2+…+an)=2Sn(n∈N+),
∴a2=1,当n≥2时,nan=2Sn-1,可得2an=(n+1)an+1-nan,化为:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+2}{n+1}$.
∴an=$\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}$•…$\frac{{a}_{3}}{{a}_{2}}•{a}_{2}$=$\frac{n+1}{n}•\frac{n}{n-1}$•…•$\frac{4}{3}×$1=$\frac{n+1}{3}$,
综上可得:an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$.
点评 本题考查了数列的递推关系、“累乘求积”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
12.甲、乙两人下棋,两人和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则乙不输的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
19.圆O1:x2+y2-6x-4y-3=0和圆O2:x2+y2-4y=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
9.“?x∈R,x2-2>0”的否定是( )
| A. | ?x∈R,x2-2<0 | B. | ?x∈R,x2-2≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$-2<0 | D. | ?x0∈R,x${\;}_{0}^{2}$-2≤0 |
13.400辆汽车通过某公路时,时速的频率分布直方图如图所示,则时速在[60,80)的汽车大约有( )
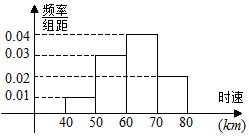

| A. | 120辆 | B. | 140辆 | C. | 160辆 | D. | 240辆 |
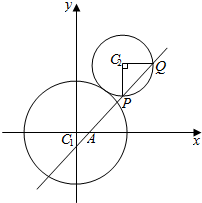 已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.
已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.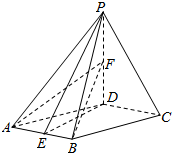 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.