题目内容
3.以下几个命题中:其中真命题的序号为③④(写出所有真命题的序号)①设A,B为两个定点,k为非零常数,|$\overrightarrow{PA}$|-|$\overrightarrow{PB}$|=k,则动点P的轨迹为双曲线;
②平面内,到定点(2,1)的距离与到定直线3x+4y-10=0的距离相等的点的轨迹是抛物线;<
③双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1$与椭圆$\frac{{x}^{2}}{35}+{y}^{2}=1$有相同的焦点;
④若方程2x2-5x+a=0的两根可分别作为椭圆和双曲线的离心率,则0<a<3.
分析 ①根据双曲线的定义知①不正确;
②说明点(2,1)在直线3x+4y-10=0上,不满足抛物线的定义;
③双曲线的离心率大于1,椭圆的离心率小于1大于0,即可判定;
④求出双曲线的焦点与椭圆的焦点,即可判定.
解答 解:①平面内与两个定点F1,F2的距离的差的绝对值等于常数k(k<|F1F2|)的点的轨迹叫做双曲线,当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,∴①不正确;
②在平面内,点(2,1)在直线3x+4y-10=0上,
∴到定点(2,1)的距离与到定直线3x+4y-10=0的距离相等的点的轨迹不是抛物线,∴②不正确;
③双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1$与椭圆$\frac{{x}^{2}}{35}+{y}^{2}=1$的焦点都是(±$\sqrt{34}$,0),有相同的焦点,正确;
④正确方程2x2-5x+a=0的可分别作为椭圆和双曲线的离心率,则$\left\{\begin{array}{l}{a>0}\\{2-5+a<0}\end{array}\right.$,∴0<a<3,正确;
故答案为:③④.
点评 本题通过命题真假的判定考查椭圆、双曲线抛物线的定义、性质和曲线的方程与方程的曲线等问题,是综合题目.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.已知函数$f(x)=1-2{cos^2}(x+\frac{π}{4})$,下列说法正确的是( )
| A. | f(x)是最小正周期为π的奇函数 | B. | f(x)是最小正周期为π的偶函数 | ||
| C. | f(x)是最小正周期为$\frac{π}{2}$的偶函数 | D. | f(x)是最小正周期为$\frac{π}{2}$的奇函数 |
18.如图是一个几何体的三视图,其俯视图是边长为3的正三角形,则该几何体的表面积为( )
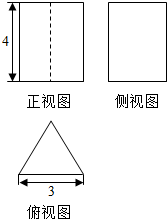

| A. | 36 | B. | 36$+\frac{9\sqrt{3}}{4}$ | C. | 36$+\frac{9\sqrt{3}}{2}$ | D. | 18$+\frac{9\sqrt{3}}{2}$ |
12.甲、乙两人下棋,两人和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则乙不输的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
13.400辆汽车通过某公路时,时速的频率分布直方图如图所示,则时速在[60,80)的汽车大约有( )
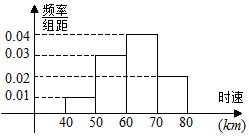

| A. | 120辆 | B. | 140辆 | C. | 160辆 | D. | 240辆 |
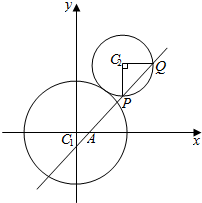 已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.
已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.