题目内容
19.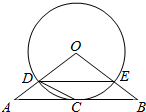 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.(l)求证:直线AB与⊙O相切;
(2)若AD=2,且tan∠ACD=$\frac{1}{3}$,求AO的长.
分析 (1)连结OC,OC⊥AB,推导出OA=OB,OC⊥AB,由此能证明直线AB与⊙O相切.
(2)延长DO交⊙O于点F,连结FC,由弦切角定理得△ACD∽△AFC,从而$\frac{CD}{PC}$=$\frac{1}{3}$,由此能求出AO的长.
解答 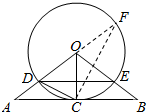 证明:(1)∵AB∥DE,∴$\frac{OA}{OD}=\frac{OB}{OE}$,又OD=OE,∴OA=OB,
证明:(1)∵AB∥DE,∴$\frac{OA}{OD}=\frac{OB}{OE}$,又OD=OE,∴OA=OB,
如图,连结OC,∵AC=CB,∴OC⊥AB,
又点C在⊙O上,∴直线AB与⊙O相切.
解:(2)如图,延长DO交⊙O于点F,连结FC,
由(1)知AB是⊙O的切线,∴弦切角∠ACD=∠F,
∴△ACD∽△AFC,∴tan∠ACD=tan∠F=$\frac{1}{3}$,
又∠DCF=90°,∴$\frac{CD}{PC}$=$\frac{1}{3}$,
∵AD=2,∴AC=6,
又AC2=AD•AF,∴2(2+2r)=62,∴r=8,
∴AO=2+8=10.
点评 本题考查线与圆相切的证明,考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质的简单运用.

练习册系列答案
相关题目
9.已知$cos(\frac{π}{4}+θ)=\frac{2}{3}\sqrt{2}$,则sin2θ=( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
10.已知圆M:(x+$\sqrt{7}$)2+y2=64,定点N($\sqrt{7}$,0),点P为圆M上的动点,点Q在NP上,点G 在线段MP上,且满足$\overrightarrow{NP}$=2$\overrightarrow{NQ}$,$\overrightarrow{GQ}$•$\overrightarrow{NP}$=0,则点G的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
7.等比数列{an}中,S2=2,S4=8,则S6=( )
| A. | -32 | B. | 32 | C. | -26 | D. | 26 |
9.“?x∈R,x2-2>0”的否定是( )
| A. | ?x∈R,x2-2<0 | B. | ?x∈R,x2-2≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$-2<0 | D. | ?x0∈R,x${\;}_{0}^{2}$-2≤0 |