Question

17．设f（x）是R上的奇函数，当x≤0时，f（x）=x²+（3a-1）x，若函数y=f（x）-|e^x-1|有两个零点，则实数a的取值范围是$（0，\frac{2}{3}]$．

Answer 1

分析 由已知求出函数解析式，把函数y=f（x）-|e^x-1|有两个零点转化为y=f（x）与y=|e^x-1|的图象有两个交点．然后分1-3a≥0和1-3a＜0画出函数图象，利用原点处曲线斜率的关系求解．

解答 解：设x＞0，则-x＜0，
∵f（x）是R上的奇函数，
∴f（x）=-f（-x）=-x²+（3a-1）x，
则f（x）=$\left\{\begin{array}{l}{{x}^{2}+（3a-1）x，x≤0}\\{-{x}^{2}+（3a-1）x，x＞0}\end{array}\right.$．
函数y=f（x）-|e^x-1|有两个零点，即y=f（x）与y=|e^x-1|的图象有两个交点．
函数f（x）=x²+（3a-1）x的两个零点为0，1-3a；函数f（x）=-x²+（3a-1）x的两个零点为0，3a-1．
当1-3a≥0，即a≤$\frac{1}{3}$时，作出函数图象如图：

f（x）=-x²+（3a-1）x与y=|e^x-1|的图象无交点，
y=1-e^x在x=0处的导数值为-e⁰=-1，函数f（x）=x²+（3a-1）x的导函数为f′（x）=2x+（3a-1）．
要使f（x）=x²+（3a-1）x的图象与y=|e^x-1|的图象有两个交点，则f′（0）=3a-1＜-1，得a＞0，
∴0＜a$≤\frac{1}{3}$；
当1-3a＜0，即a＞$\frac{1}{3}$时，作出函数图象如图：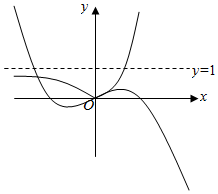

f（x）=x²+（3a-1）x的图象与y=|e^x-1|的图象有2个交点，
y=e^x-1在x=0处的导数值为e⁰=1，函数f（x）=-x²+（3a-1）x的导函数f′（x）=-2x+（3a-1）．
要使f（x）=-x²+（3a-1）x与y=|e^x-1|的图象无交点，则f′（0）=3a-1≤1，得a$≤\frac{2}{3}$．
∴$\frac{1}{3}＜a≤\frac{2}{3}$．
综上，若函数y=f（x）-|e^x-1|有两个零点，则实数a的取值范围是（0，$\frac{2}{3}$]．
故答案为：（0，$\frac{2}{3}$]．

点评 本题考查根的存在性与根的个数判断，考查数学转化思想方法与数形结合的解题思想方法，是压轴题．