题目内容
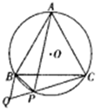 如图,圆O是等边三角形ABC的外接圆,点P在劣弧
如图,圆O是等边三角形ABC的外接圆,点P在劣弧 |
| BC |
(Ⅰ)求证:CQ=AP;
(Ⅱ)当点P是劣弧
 |
| BC |
考点:与圆有关的比例线段
专题:综合题,立体几何
分析:(Ⅰ)证明△ABP≌△CBQ,可得CQ=AP;
(Ⅱ)设AB=1,求出∠ABP=90°,∠APB=60°,可得BP,利用S△ABC:S△BPQ=AB2:BP2,可得结论.
(Ⅱ)设AB=1,求出∠ABP=90°,∠APB=60°,可得BP,利用S△ABC:S△BPQ=AB2:BP2,可得结论.
解答:
(Ⅰ)证明:∵A,B,C,P共圆,△ABC为等边三角形,
∴∠QPB=∠BAC=60°,AB=BC…(1分)
∵PQ=PB,∴△QPB为等边三角形,
∴∠Q=∠BPA=∠BCA=60°…(2分)
∴△ABP≌△CBQ…(3分)
∴CQ=AP;…(4分)
(Ⅱ)解:设AB=1,
∵点P是劣弧
的中点,AB=AC,
∴∠ABP=90°,∠APB=60°,…(6分)
∴BP=
,…(8分)
∴S△ABC:S△BPQ=AB2:BP2=3…(10分)
∴∠QPB=∠BAC=60°,AB=BC…(1分)
∵PQ=PB,∴△QPB为等边三角形,
∴∠Q=∠BPA=∠BCA=60°…(2分)
∴△ABP≌△CBQ…(3分)
∴CQ=AP;…(4分)
(Ⅱ)解:设AB=1,
∵点P是劣弧
 |
| BC |
∴∠ABP=90°,∠APB=60°,…(6分)
∴BP=
| ||
| 3 |
∴S△ABC:S△BPQ=AB2:BP2=3…(10分)
点评:本题考查四点共圆,考查三角形全等的判断与运用,考查三角形面积的计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设n=
4sinxdx,则二项式(x-
)n的展开式的常数项是( )
| ∫ |
0 |
| 1 |
| x |
| A、12 | B、-2 | C、4 | D、1 |
若△ABC的内角A、B、C的对边分别是a、b、c,且asinA+csinC-bsinB=
asinC,则cosB等于( )
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
 某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.
某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.