题目内容
15.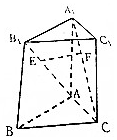 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积) |
分析 由题意画出图形,取特殊点得到M的轨迹为平行四边形区域,再由三角形面积求解.
解答 解:当E位于B1,A,而F在A1C上移动时,M的轨迹为平行于A1C的两条线段,
当F位于A1,C,而E在AB1上移动时,M的轨迹为平行与AB1的两条线段.
其它情况下,M的轨迹构成图中平行四边形内部区域.
∴|L|=2×$\frac{1}{2}$|$\frac{1}{2}$AB1|•|$\frac{1}{2}$CA1|•sinθ=$\frac{1}{4}$|AB1|•|CA1|•sinθ.
故选:C.
点评 本题考查棱柱的结构特征,考查空间想象能力和思维能力,利用特殊点得到M的轨迹是解答该题的关键,是压轴题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
7.已知函数f(x)=Asin(2x+φ)-$\frac{1}{2}$(A>0,0<φ<$\frac{π}{2}$)的图象在y轴上的截距为1,且关于直线x=$\frac{π}{12}$对称,若对于任意的x∈[0,$\frac{π}{2}$],都有m2-3m≤f(x),则实数m的取值范围为( )
| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
5.已知函数f ( x)=2ax-a+3,若?x0∈(-1,1),f ( x0 )=0,则实数 a 的取值范围是( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3) | C. | (-3,1) | D. | (1,+∞) |
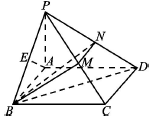 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.