题目内容
10.“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 利用直线与直线的平行条件得出k1=k2,结合充分必要条件判断即可.
解答 解:若“a=3”成立,则两直线的方程分别是3x-2y-1=0与6x-4y+1=0,k1=k2=$\frac{3}{2}$.
所以两直线一定平行;
反之,当“直线ax-2y-1=0与直线6x-4y+1=0平行”成立时,有$\frac{a}{6}$=$\frac{1}{2}$,所以a=3;
所以“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的必要充分条件,
故选:A.
点评 本题简单的考查了直线的平行的条件,充分必要条件的概念,难度不大,属于容易题.

练习册系列答案
相关题目
15.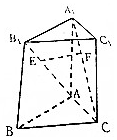 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积) |
19.椭圆E的焦点在x轴上,中心在原点,其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点,则椭圆E的标准方程为( )
| A. | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B. | $\frac{x^2}{2}+{y^2}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D. | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
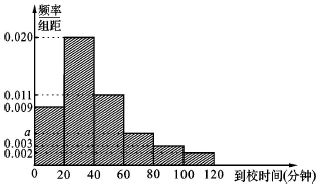 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: