题目内容

5．已知函数f （ x）=2ax-a+3，若?x0∈（-1，1），f （ x0 ）=0，则实数 a 的取值范围是（　　）
A．（-∞，-3）∪（1，+∞）B．（-∞，-3）C．（-3，1）D．（1，+∞）

分析 利用零点判定定理以及一次函数的性质，列出不等式求解即可．

解答 解：函数f （ x）=2ax-a+3，若?x0∈（-1，1），f （ x0 ）=0，
可得（-3a+3）（a+3）＜0，解得a∈（-∞，-3）∪（1，+∞）．
故选：A．

点评 本题考查零点判定定理的应用，函数的性质的应用，考查计算能力．

练习册系列答案
相关题目
15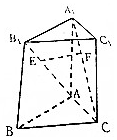．如图，在三棱柱ABC-A1B1C1中，已知E，F分别是线段AB1与CA1上的动点，异面直线AB1与CA1所成角为θ，记线段EF中点M的轨边为L，则|L|等于（　　）
A．$\frac{1}{2}$|AB1|
B．$\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-（\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}}）^{2}}$
C．$\frac{1}{4}$|AB1|•|CA1|•sinθ
D．$\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$（V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积）
16．直线m经过抛物线C：y2=4x的焦点F，与C交于A，B两点，且|AF|+|BF|=10，则线段AB的中点D到y轴的距离为4．
13．已知F1，F2是椭圆与双曲线的公共焦点，P是它们的一个公共点，且|PF1|＞|PF2|，线段PF1的垂直平分线过F2，若椭圆的离心率为e1，双曲线的离心率为e2，则$\frac{2}{e_1}+\frac{e_2}{2}$的最小值为（　　）
A．$\sqrt{6}$B．3C．6D．$\sqrt{3}$
20．在直角坐标系xoy中，曲线C的参数方程为$\left\{\begin{array}{l}x=acost\\ y=2sint\end{array}\right.$（t为参数，a＞0）以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，已知直线l的极坐标方程为$ρcos（{θ+\frac{π}{4}}）=-2\sqrt{2}$．
（Ⅰ）设P是曲线C上的一个动点，当a=2时，求点P到直线l的距离的最小值；
（Ⅱ）若曲线C上的所有点均在直线l的右下方，求a的取值范围．
10．在锐角三角形ABC 中，角 A，B，C 的对边分别为 a，b，c．若a=2bsinC，则tanA+tanB+tanC的最小值是（　　）
A．4B．$3\sqrt{3}$C．8D．$6\sqrt{3}$
17．设全集U={-2，-1，0，1，2}，A={x|x≤1}，B={-2，0，2}，则∁U（A∩B）=（　　）
A．{-2，0}B．{-2，0，2}C．{-1，1，2}D．{-1，0，2}
14．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{x+y≥0}\\{x+2y-4≥0}\end{array}\right.$，则z=x-2y的最大值为（　　）
A．-12B．-1C．0D．$\frac{3}{2}$
15．下列命题中真命题是（　　）
A．$?x∈（{-∞，\frac{π}{4}}），tanx≤1$
B．设l，m表示不同的直线，α表示平面，若m∥l且m⊥α，则l∥α
C．利用计算机产生0和l之间的均匀随机数m，则事件“3m-1≥0”发生的概率为$\frac{1}{3}$
D．“a＞0，b＞0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网