题目内容
1.若函数$f(x)=|{\frac{e^x}{2}-\frac{a}{e^x}}|({a∈R})$在区间[1,2]上单调递增,则实数a的取值范围是[-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$].分析 去掉绝对值,根据f′(x)≥0,得到a的范围即可.
解答 解:f(x)=$|\frac{{e}^{2x}-2a}{{2e}^{x}}|$;
∵x∈[1,2];
∴a≤$\frac{{e}^{2}}{2}$时,f(x)=$\frac{{e}^{2x}-2a}{{2e}^{x}}$,f′(x)=$\frac{{e}^{2x}+2a}{{2e}^{x}}$;
由f′(x)≥0;解得:a≥-$\frac{{e}^{2x}}{2}$≥-$\frac{{e}^{2}}{2}$,
即-$\frac{{e}^{2}}{2}$≤a≤$\frac{{e}^{2}}{2}$时,f′(x)≥0,f(x)在[1,2]上单调递增;
即a的取值范围是:[-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$].
故答案为:[-$\frac{{e}^{2}}{2}$,$\frac{{e}^{2}}{2}$].
点评 考查对含绝对值函数的处理方法:去绝对值,根据函数导数符号判断函数单调性的方法,以及指数函数的单调性.

练习册系列答案
相关题目
11.复数z=$\frac{(i-1)^{2}+2}{i+1}$的实部为( )
| A. | -2 | B. | -1 | C. | 1、 | D. | 0 |
12.已知圆C方程x2+y2-2x-4y+a=0,圆C与直线x+2y-4=0相交于A,B两点,且OA⊥OB(O为坐标原点),则实数a的值为( )
| A. | $-\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{1}{5}$ |
13.设l,m,n表示三条直线,α,β,γ表示三个平面,则下面命题中不成立的是( )
| A. | 若l⊥α.m⊥α,则l∥m | |
| B. | 若m?β,m⊥l,n是l在β内的射影,则m⊥n | |
| C. | 若m?α,n?α,m∥n,则n∥α | |
| D. | 若α⊥γ,β⊥γ,则α∥β. |
10.书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
15.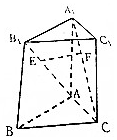 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积) |
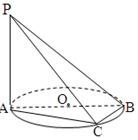 已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,
已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,