题目内容
2.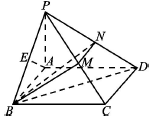 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.(1)求证:PA⊥平面ABCD;
(2)若M,N分别为棱PC,PD中点,求四棱锥B-MCDN的体积.
分析 (1)推导出PA⊥AB,BC⊥PA,由此能证明PA⊥平面ABCD.
(2)四棱锥B-MCDN的体积VB-MCDN=VA-MCDN=$\frac{3}{4}{V}_{A-PCD}=\frac{3}{4}{V}_{P-ACD}$,由此能求出结果.
解答 证明:(1)由题意有PA2+AB2=3+3=6=PB2,所以PA⊥AB①,
因为AB=AP,E为PB中点,
所以AE⊥PB,又AE⊥PC,PB∩PC=C,
所以,AE⊥平面PBC,
又BC?平面PBC,所以AE⊥BC,
又AB⊥BC,及AE∩AB=A,
所以BC⊥平面PAB,
又PA?平面PAB,所以BC⊥PA②,
由①②及AB∩BC=B得PA⊥平面ABCD,
故PA⊥平面ABCD.
解:(2)因为BA∥CD,CD?平面PCD,
所以BA∥平面PCD,
所以四棱锥B-MCDN的体积VB-MCDN=VA-MCDN,
又M,N分别为棱PC,PD的中点,所以${S_{MCDN}}=\frac{3}{4}{S_{PCD}}$,
所以${V_{B-MCDN}}={V_{A-MCDN}}=\frac{3}{4}{V_{A-PCD}}=\frac{3}{4}{V_{P-ACD}}=\frac{3}{4}×\frac{1}{3}×({\frac{1}{2}×2×\sqrt{3}})×\sqrt{3}=\frac{3}{4}$.
点评 本题考查线面垂直的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12.已知圆C方程x2+y2-2x-4y+a=0,圆C与直线x+2y-4=0相交于A,B两点,且OA⊥OB(O为坐标原点),则实数a的值为( )
| A. | $-\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{1}{5}$ |
13.设l,m,n表示三条直线,α,β,γ表示三个平面,则下面命题中不成立的是( )
| A. | 若l⊥α.m⊥α,则l∥m | |
| B. | 若m?β,m⊥l,n是l在β内的射影,则m⊥n | |
| C. | 若m?α,n?α,m∥n,则n∥α | |
| D. | 若α⊥γ,β⊥γ,则α∥β. |
10.书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
7.一个车间为了规定工时定额,需要确定加工零件所花费的时间,由此进行了5次实验,收集数据如下:
由以上数据的线性回归方程估计加工100个零件所花费的时间为( )
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 零件数:x个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间:y分钟 | 59 | 71 | 75 | 81 | 89 |
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | 124分钟 | B. | 150分钟 | C. | 162分钟 | D. | 178分钟 |
15.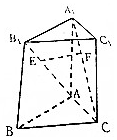 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积) |
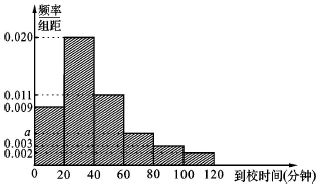 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: